Das Delta eine Option

Der Schlüssel zum Erfolg im Optionshandel ist die Greeks einer Option zu verstehen und der vielleicht wichtigste Greek von allen ist das Delta. Was sich hinter dem Delta einer Option verbirgt und wie ihr es in euren täglichen Optionshandel nutzen könnt, verrate ich euch in diesen Artikel.

Dieser Artikel behandelt das Delta einer Option im Detail. Wenn ihr gern einen allgemeineren Überblick über alle Griechen einer Optionen haben wollt, dann könnt ihr euch auch diesen Artikel von mir durchlesen.

Was ist das Delta einer Option?

Das Delta einer Option ist für viele Optionshändler der wahrscheinlich wichtigste Greek. Es gibt an, um wie viel sich der Preis der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt und gibt Optionshändlern damit Auskunft darüber, wie sehr die Wertentwicklung einer Option von den Preisbewegungen des Underlying abhängig ist.

Der Wert des Deltas kann immer nur zwischen -1 und +1 liegen wobei für Calls und Puts immer gilt:

• Bei Calls ist das Delta der Option immer zwischen 0 bis 1
• Bei Puts ist das Delta der Option immer zwischen -1 bis 0

Hat eine Call Option somit ein Delta von 0,5, dann steigt der Wert der Option um 50 Cent, wenn das Underlying um einen Euro im Wert steigt. Hat eine Put Option im Gegensatz dazu ein Delta von -0,5, dann fällt der Wert des Puts um 50 Cent, wenn der Preis des Underlyings um einen Euro steigt.

Die Dezimalschreibweiße ist zwar die mathematisch korrekte Art, das Delta zu beschreiben aber in der Praxis sagt bzw. schreibt man selten, dass eine Option ein Delta von 0,5 oder -0,5 hat, sondern man sagt stattdessen, dass eine Option ein Delta von 50 oder -50 hat.

Ein Delta von 10 bedeutet somit, dass eine Call Option 10 Cent im Wert steigt, wenn das Underlying einen Euro im Wert ansteigt.

Ganz wichtig ist allerdings, dass solche Rechnungen nur Annäherungen an die tatsächliche Preisänderung des Optionspreises sind. Das Delta einer Option ist schließlich keine statische Kennzahl und kann durch viele Faktoren beeinflusst werden (mehr dazu gleich) und entsprechend kann man die Preisänderung einer Option mithilfe des Deltas nur für geringe Preisänderungen des Underlyings berechnen. Lasst mich das ganze einfach anhand eines kleines Beispiels verdeutlichen.

Wie sehr sich das Delta einer Option durch eine Änderung des Underlying-Preises verändert, gibt das sogenannte Gamma an. Das ist ein weitere Greek, den ich euch in einem anderen Artikel erklären werde aber ihr könnt ihn euch einfach als das Delta des Deltas vorstellen. D.h. das Delta gibt an, wie sehr sich der Preis der Option verändert, wenn sich der Preis des Underlyings ändert und das Gamma gibt an, wie sehr sich das Delta ändert, wenn sich der Preis des Underlyings ändert.

Von allen Faktoren, die das Delta beeinflussen (mehr dazu gleich) hat der Preis des Underlyings bzw. die sogenannte „Moneyness“ den größten Einfluss auf das Delta.

Als allgemeine Faustregel gilt, dass Optionen, die sich im Geld (ITM) befinden, ein Delta größer 50 haben und Optionen, die sich außerhalb des Geldes (OTM) befinden ein Delta kleiner 50 haben. Optionen, die sich am Geld (ATM) befinden, haben ein Delta von circa 50.

Umso mehr sich eine Call Option im Geld befindet, desto mehr nähert sich das Delta der Option an 1 an und je mehr sich eine Call Option außerhalb des Geldes befindet, desto stärker nähert sich das Delta der Option an 0 an. Bei Put Optionen verhält es sich genauso, allerdings nähert sich das Delta von Put Optionen immer mehr -1 an, je stärker die Option sich ins Geld bewegt und immer näher 0, je weiter sich die Option aus dem Geld bewegt.

Beträgt der Marktpreis des Underlyings genau dem Strikepreis einer Option (also die Option ist exakt am Geld), dann ist das Delta der Option allerdings in aller Regel nicht genau 50. Überlicherweise haben Call Optionen in dem Fall ein Delta von leicht mehr als 50 und Put Optionen ein Delta von leicht weniger als 50.

Der Effekt bzw. Abstand zwischen dem Delta einer Call und Put Option mit gleichem Ausübunsgpreis wird dabei umso größer je länger die Laufzeit der Option ist (mehr dazu weiter unten) und je höher der aktuelle Marktzins ist. Grund dafür ist die sogenannte „Put-Call-Parität“ die ich euch in einem anderen Artikel erklären werde.

Habt ihr übrigens eine Position, die aus mehreren Optionen besteht, dann ist das Delta dieser Position die Summe aller Deltas der Optionen, die ihr haltet. Handelt ihr also komplexere Optionsstrategien, dann kann es schnell auch kompliziert werden zu wissen, wie sich das Delta bei Kursschwankungen bewegen wird. Damit ihr nicht den Überblick verliert, habe ich deshalb für euch ein Cheat Sheet erstellt, das euch direkt zeigt, wie sich das Delta für verschiedene Optionsstrategien verändert, je nachdem wie sich der Markt bewegt. Ihr könnt es euch hier gratis herunterladen.

Die Berechnung des Deltas einer Option

Um das Delta einer Option zu berechnen, gibt es grundsätzlich zwei Möglichkeiten. Die korrekte Variante ist, dass man das Delta mithilfe eines Optionspreismodells berechnet und die weniger komplizierte Variante ist die Berechnung mithilfe von Marktdaten. Ich erkläre euch gleich beide Varianten etwas genauer, allerdings will ich an dieser Stelle auch hinweisen, dass es in aller Regel gar nicht notwendig ist, dass ihr das Delta einer Option selbst berechnet, weil ihr diese Information auch online auf verschiedenen Webseiten einsehen könnt oder einfach mithilfe meines Optionspreisrechners selbst berechnen könnt bzw. ein guter Broker euch die Information auch immer bereitstellt.

Ich nutze für den Optionshandel zum Beispiel den Broker Estably (bis vor kurzem noch unter „Banx Broker“ bekannt) und dort wird das Delta als Standardinformation bei jeder Option direkt mit angezeigt. D.h. noch bevor ich überhaupt eine Option kaufe oder verkaufe, erhalte ich alle Informationen direkt von meinem Broker, die ich benötige.

Das Delta wird bei eurem Broker dabei in der sogenannten Option Chain angezeigt. Dort findet ihr alle Call und Put Optionen geordnet nach dem jeweiligen Strike Preis für eine bestimmte Laufzeit. Neben dem Preis für jede Option werden in der Option Chain aber auch alle Greeks inklusive dem Delta angezeigt. Hier mal ein Screenshot, wie das ganze bei Estably aussieht.

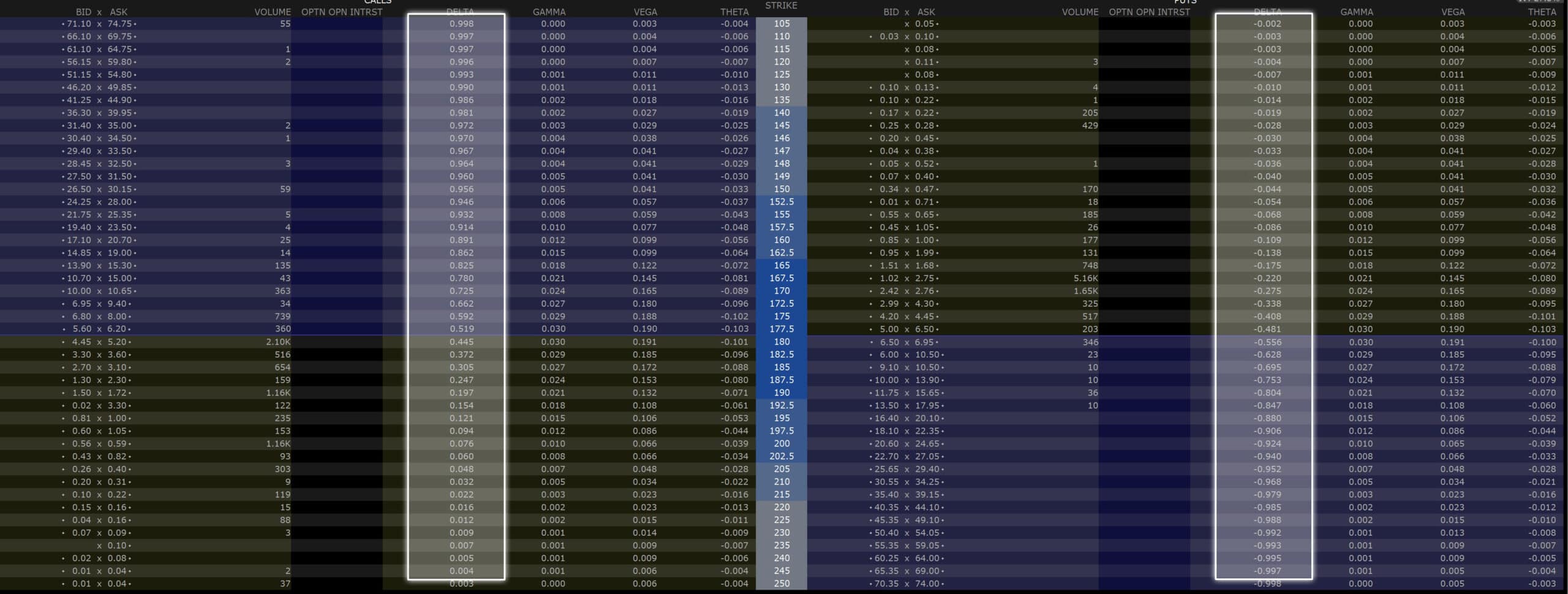
Wenn ihr auch Optionen handeln möchtet, dann kann ich euch Estably wirklich nur empfehlen. Im Hintergrund nutzt Estably Interactive Brokers was ein Tool ist, das auch von Profis genutzt wird. Entsprechend bekommt ihr dort alle Informationen, die für den Optionshandel notwendig sind und könnt euch auch alles so individuell einrichten, wie ihr möchtet.

Wenn ihr ein Depot bei Estably eröffnen wollt, dann könnt ihr das über diesen Link machen*. Das gibt euch Zugriff auf ein wirklich tolles Trading Tool, einen günstigen Broker und ihr unterstützt gleichzeitig noch meine Arbeit, weil ich bei einer Depoteröffnung eine kleine Gebühr von Estably bekomme (ohne, dass das ganze für euch teurer wird).

Aber zurück zum Thema. Auch wenn ihr das Delta einer Option selbst nicht berechnen müsst, ist es dennoch ganz gut zu wissen, wie es berechnet wird, damit ihr besser verstehen könnt wie sich das Delta einer Option verändert je nachdem welche Marktveränderungen eintreten.

Mithilfe eines Optionspreismodells

Grundsätzlich gibt es verschiedene mathematische Modelle zur Preisberechnung von Optionen, allerdings hat sich in der Praxis das sogenannte „Black-Scholes-Modell“ durchgesetzt, dass nach den beiden US-Amerikaner Fischer Black und Myron Scholes benannt wurde, die dieses Modell 1973 veröffentlichten.

Das besondere am Black-Scholes Modell ist, dass es ermöglichte, die Preisberechnung einer Option auf eine mehr oder weniger einfache mathematische Formel herunterzubrechen, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.

Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt.

Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.

Das Delta ist dabei die erste Ableitung des Black-Scholes Modells nach dem Preis des Underlyings weswegen das Delta auch angibt, um wie viel sich der Preis der Option ändert, wenn sich der Wert des Underlyings um 1 erhöht oder verringert.

Die Formel bzw. besser gesagt Formeln für das Black-Scholes Modell sind relativ komplex und ich möchte hier auch nicht zu sehr ins Detail gehen, weswegen ich einfach auf Wikipedia verweisen würde, wenn ihr gern mehr dazu erfahren wollt.

Mithilfe von Marktbeobachtungen

Man kann das Delta aber auch grob schätzen, indem man einfach am Markt die Preise einer Option beobachtet und schaut, wie der Preis der Option auf kleine Änderungen des Underlyings reagiert.

Ihr benötigt dazu einfach nur zwei unterschiedliche Preise des Underlyings und schaut dann wie bei beiden Preisen der Preis der Option war. Bildet mit diesem Wissen dann einfach die Differenz zwischen den beiden Optionspreisen und den beiden Preisen des Underlyings und teilt dann die Differenz des Optionspreises durch die Differenz des Underlying-Preises.

Das Ergebnis ist das Delta, allerdings solltet ihr diese Methode nur bei kleinen Preisänderungen des Underlyings verwenden, weil ihr bei zu großen Änderungen ansonsten zu große Abweichungen zum tatsächlichen Delta bekommt. Nutzt also nur Differenzen von maximal einem Euro oder einem Dollar.

Andere Interpretationen des Delta

Wie oben schon erwähnt, beschreibt das Delta einer Option wie stark sich der Wert einer Option verändert, wenn sich der Preis des Underlyings um eine Währungseinheit verändert. Es gibt allerdings auch noch weitere Möglichkeiten, wie das Delta einer Option interpretiert werden kann.

1. Das Äquivalent zu einem Direktinvestment in das Underlying

Das Delta gibt an, wie stark sich eine Option in Abhängigkeit vom Underlying ändert. Beträgt das Delta 0, dann ändert sich der Optionspreis überhaupt nicht bei einer Änderung des Underlying-Preises und bei einem Delta von 1, dann verändert sich der Wert der Option um einen Euro, wenn sich der Wert des Underlying um einen Euro bewegt.

Nach dieser Logik kann man also sagen, dass das Underlying selbst immer ein Delta von 1 hat. Immer wenn sich der Kurs des Underlyings um einen Euro bewegt, dann ist das Underlying auch einen Euro mehr oder weniger wert.

Besitze ich eine Call Option mit einem Delta von 60, dann steigt der Wert meiner Option um 60 Cent, wenn sich das Underlying um einen Euro erhöht. Da Optionen in aller Regel aber 100 Aktien umfassen, würde der Wert der Call Option also in dem Fall um 60 EUR steigen, wenn der Kurs des Underlyings um einen Euro steigt.

Die Wertentwicklung meiner Option ist in diesem Fall also genau so als würde ich genau 60 Aktien des Underylings besitzen. Steigt der Wert der 60 Aktie um einen Euro, dann mache ich mit den Aktien 60 Euro Gewinn und steigt der Wert der Aktie um einen Euro, dann steigt auch der Wert der Option um 60 EUR.

Das Delta einer Option entspricht somit auch dem Äquivalent zu einem Direktinvestment in das Underlying. Diese Interpretation ist vor allem beim sogenannten „Delta Hedging“ wichtig, dass ich euch in diesem Artikel genauer erkläre.

2. Die Wahrscheinlichkeit, dass sich die Option am Ende der Laufzeit im Geld befindet

In der Praxis wird das Delta einer Option auch als grobe Annäherung dafür genutzt, wie wahrscheinlich es ist, dass sich die Option am Ende der Laufzeit im Geld befindet oder nicht. Eine Call Option mit einem Delta von 75 hätte in diesem Fall also grob eine Wahrscheinlichkeit von 75%, dass sie sich bei Laufzeitende im Geld befindet.

Das macht intuitiv erst einmal auch Sinn. Optionen mit einem hohen Delta (größer 50) befinden sich schließlich schon im Geld und haben deswegen auch eine höhere Wahrscheinlichkeit am Ende der Laufzeit weiterhin im Geld zu sein. Optionen mit niedrigem Delta (kleiner 50) befinden sich aktuell außerhalb des Geldes und haben dementsprechend auch nur eine geringere Wahrscheinlichkeit sich ins Geld zu bewegen.

Mathematisch betrachtet, ist diese Faustregel aber wirklich nicht mehr als eine ganz grobe Annäherung und ihr solltet sie mir Vorsicht genießen. Weil ich die Praktiker unter euch nicht mit Mathematik langweilen möchte, müsst ihr den folgenden Text aufklappen, um zu verstehen warum das so ist, allerdings kann ich jedem Optionshändler nur empfehlen, diesen Zusammenhang unbedingt zu verstehen.

Warum das Delta nur eine Annäherung an die ITM Wahrscheinlichkeit ist

In der Black-Scholes-Formel entspricht das Delta der Option dem Wert der Normalverteilung für den Faktor D1. Die Wahrscheinlichkeit, dass eine Option im Geld landet ist wiederum der Wert der Normalverteilung für den Faktor D1 abzüglich der impliziten Volatilität multipliziert mit der Wurzel aus der Restlaufzeit.

D.h. rein mathematisch betrachtet ist die Wahrscheinlichkeit für eine Option im Geld zu landen und deren Delta zwar etwas komplett anderes aber auch nicht so unterschiedlich. Die beiden Werte unterscheiden sich dabei umso mehr, je länger die Laufzeit der Option ist und je größer die implizite Volatilität ist.

Für kurze Laufzeiten und Optionen mit geringer impliziter Volatilität ist das Delta also eine sehr gute Annäherung für die Wahrscheinlichkeit einer Option im Geld zu landen aber je länger die Laufzeit ist und je höher die Volatilität ist, desto mehr solltet ihr das ganze mit Vorsicht genießen.

Wie gut diese Faustregel in der Praxis zutrifft, habe ich einmal selbst mithilfe von über 500.000 Optionen analysiert. Die folgende Grafik zeigt euch dabei auf der Y-Achse, wie hoch das Delta zum Kaufzeitpunkt der Option war (und entsprechend die grobe Wahrscheinlichkeit, dass die Option im Geld landet) und auf der X-Achse wie viele Optionen mit dem Delta am Ende wirklich im Geld landete.

Die rote Linie zeigt euch dabei den Verlauf, wenn das Delta einer Option die Wahrscheinlichkeit im Geld zu landen immer korrekt angeben würde. Die grüne Linie zeigt euch aber stattdessen die tatsächliche Wahrscheinlichkeit aller Call Optionen, die ich untersucht habe und die blaue Linie zeigt euch die tatsächliche Wahrscheinlichkeit aller Put Optionen.

Ihr seht dabei schön deutlich, dass vor allem bei Optionen, die sich entweder weit im oder weit außerhalb des Geldes befinden, dass Delta eine sehr gute Annäherung für die Wahrscheinlichkeit ist, dass die Option im Geld landet.

Das Delta gibt die Wahrscheinlichkeit aber umso schlechter an, je näher sich eine Option am Geld befindet und zur großen Überraschung gibt es dabei einen sehr wichtigen Unterschied zwischen Put und Call Optionen.

Bei ATM Call Optionen unterschätzt das Delta nämlich tendenziell die Wahrscheinlichkeit, dass eine Option im Geld landet. D.h. ATM Call Optionen landen viel häufiger im Geld, als es das Delta vermuten lässt und bei Put Optionen ist es genau anders herum. Für Put ATM Optionen überschätzt das Delta nämlich tendenziell die Wahrscheinlich, dass eine Option im Geld landet. D.h. Put Optionen landen viel seltener im Geld, als es das Delta vermuten lässt.

3. Der Anstieg der Tangente des Gewinn-und-Verlust Profils der Option

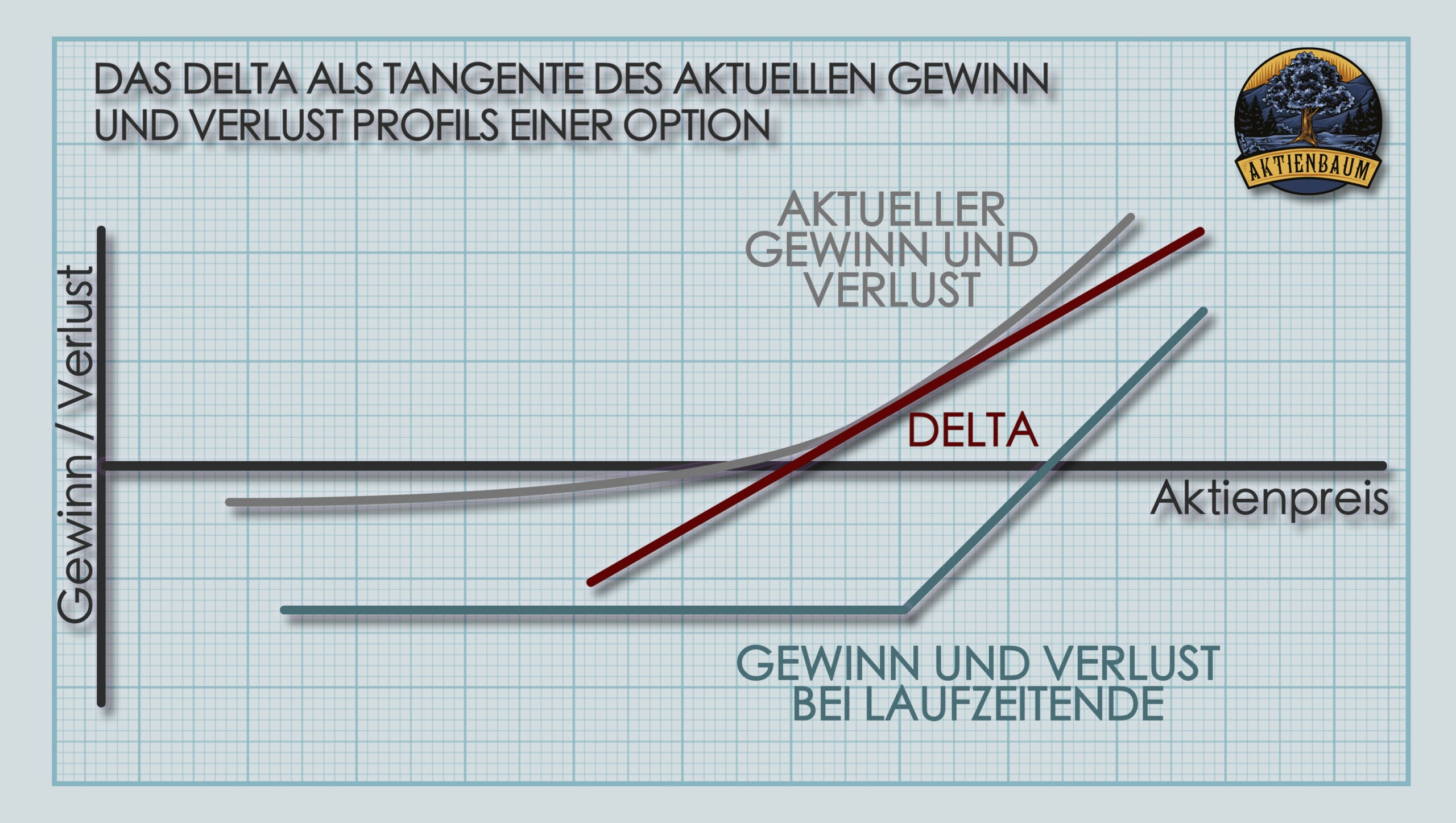
Das Delta kann aber auch grafisch interpretiert werden, wenn man sich dazu den typischen Verlauf des Gewinn und Verlustes einer Option anschaut, wie ich es euch in der unteren Grafik anhand einer Call Option zeige.

Legt man an die Grafik eine Tangente an, also eine Linie, die die Grafik in nur einen Punkt schneidet, dann sagt der Anstieg dieser Tangente aus, wie sehr sich der Wert der Option verändert, wenn sich der Wert des Underlyings leicht erhöht oder verringert.

Das ist auch genau die Definition des Deltas, weswegen der Anstieg der Tangente somit auch dem Delta der Option entspricht. Bewegt sich die Option immer mehr ins Geld hinein, dann ist der Anstieg der Tange auch immer größer bzw. nähert er sich immer mehr 1 an, genau wie wir oben auch schon beim Delta gesehen haben.

Fällt der Wert des Underlyings aber, dann verringert sich der Anstieg der Tangente immer mehr und nähert sich null an, wie es auch bei dem Delta der Fall ist.

Weiter oben habe ich euch schon gesagt, dass das Delta nichts anderes ist als die erste Ableitung der Black-Scholes Formel nach dem Preis ist und grafisch betrachtet, ist das auch die selbe Definition der Tangente.

Der Zusammenhang des Delta mit anderen Markteinflüssen

Volatilität

Die Volatilität, also die übliche Schwankungsbreite des Underlyings, hat einen großen Einfluss auf das Delta einer Option. Ist die Volatilität gering, dann ist das Delta von In-the-Money Optionen, höher und für Out-of-the-Money Optionen niedriger als bei einer Option mit hoher Volatilität des Underlyings. Ihr könnt den Zusammenhang sehr gut in der folgenden Grafik sehen.

Die Grafik zeigt euch dabei den Verlauf des Delta zweier Call Optionen in Abhängigkeit von der Moneyness der Option und deren Volatilität.

Die rote Linie ist dabei die Option mit hoher Volatilität und die blaue Linie die Option mit der niedrigen Volatilität. Beide Optionen beziehen sich auf das selbe Underlying, haben die selbe Laufzeit und in beiden Fällen ist der Preis des Underlyings gerade 50 EUR. Das einzige, was variabel ist, ist der Strike Preis.

Ihr seht dabei deutlich, dass die Option mit der geringen Volatilität ein höheres Delta im Vergleich zu der Option mit hoher Volatilität hat, wenn die Option im Geld ist aber dafür ein geringeres Delta, wenn die Option nicht im Geld ist.

Restlaufzeit

Die Restlaufzeit einer Option hat ebenso einen großen Einfluss auf das Delta. Ist die Restlaufzeit nur noch kurz , dann ist das Delta von In-the-Money Optionen höher und für Out-of-the-Money Optionen niedriger als bei einer Option mit einer längeren Restlaufzeit. Ihr könnt den Zusammenhang wieder sehr gut in der folgenden Grafik sehen.

Die Grafik zeigt euch dabei wieder den Verlauf des Deltas von drei Call Optionen in Abhängigkeit von der Moneyness der Option und deren Restlaufzeit.

Die blaue Linie ist dabei die Option mit der kürzesten Restlaufzeit (3 Monate), die grüne Linie hat eine etwas längere Laufzeit (6 Monate) und die rote Linie hat die längste Laufzeit (12 Monate).

Ihr könnt dabei erkennen, dass das Delta einer Option im Geld umso höher ist, je kürzer die Restlaufzeit ist und für OTM Option dafür umso niedriger ist, je kürzer die Restlaufzeit ist.

Allgemein kann man sagen, dass umso länger die Laufzeit einer Option ist, desto stärker nähert sich das Delta für alle Optionen (im Geld, am Geld und aus dem Geld) an 0,5 an.

Besonders deutlich kann man diesen Zusammenhang auch in der nächsten Grafik sehen.

Die Grafik zeigt euch diesmal das Delta einer Call Option an, die dich gerade am Geld befindet. In der Grafik werden alle Einflussgrößen gleich gelassen und nur die Restlaufzeit verändert und ihr könnt sehen, was das für einen Einfluss auf das Delta der Call Option hat.

Während das Delta der ATM Call Option bei langer Laufzeit noch über 50 liegt, nähert es sich bei kürzer werdender Laufzeit immer mehr einem Delta von genau 50 an. Ihr seht aber auch, dass sich das Delta einer Option umso schneller verringert, je näher man sich an das Laufzeitende bewegt.

Ihr müsst euch also merken, dass selbst wenn alle Faktoren einer Option gleich bleiben und sich auch der Kurs des Underlyings nicht verändert, das Delta sich dennoch verändert, einfach nur weil sich mit jeden Tag die Restlaufzeit der Option verkürzt.