Ein entscheidender Faktor für Erfolg im Optionshandel ist das Verständnis der Griechen, und unter diesen spielt das Gamma eine wesentliche Rolle. In diesem Artikel erkläre ich, was das Gamma einer Option bedeutet und wie ihr dieses Wissen effektiv in eurem täglichen Handel mit Optionen einsetzen könnt.
💡Das Wichtigste in Kürze
Dieser Artikel behandelt das Gamma einer Option im Detail. Wenn ihr gern einen allgemeineren Überblick über alle Griechen einer Optionen haben wollt, dann könnt ihr euch auch diesen Artikel von mir durchlesen.
Was ist das Gamma
Das Gamma einer Option gibt an, um wieviel sich das Delta der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt. D.h. bei einem Delta von 0,3 und einem Gamma von 0,1 würde das Delta der Option um 0,1 auf 0,4 steigen, wenn sich der Wert des Underlyings um einen Euro erhöht.
Das Gamma einer Option kann dabei zwischen 0 und 1 liegen und da es sich um einen absoluten Wert handelt, gibt es auch keinen Unterschied bei Puts und Calls. D.h. ein Gamma von 0,1 erhöht immer das Delta einer Option um 0,1 bei einem Preisanstieg des Underlyings um eine Währungseinheit ganz egal ob Put oder Call oder Long oder Short.
Unter identischen Rahmenbedingungen, d.h. bei gleichem Strike-Preis, gleichem Underlying Kurs, gleicher Laufzeit, gleichem Zinssatz usw., ist das Gamma eines Calls und eines Puts sogar identisch.
🔥 Gut zu wissen
Als Gamma Long bezeichnet man eine Position, bei der das Gamma der Option ansteigt, wenn der Kurs des Underlyings steigt. Das ist dann der Fall, wenn man eine Call oder Put Option kauft (Long Position).
Im Gegensatz dazu spricht man von Gamma Short, wenn das Gamma einer Option fällt, wenn sich der Kurs des Underlyings verringert. Das ist immer dann der Fall, wenn man eine Call oder Put Option verkauft (Short Position).
Weil das Gamma nur zwischen 0 und 1 sein kann, kann man es aber auch als Prozentwert interpretieren in Abhängigkeit vom Kurs des Underlyings. Hat eine Option also ein Gamma von 0,05 und der Kurs des Underlyings erhöht sich um 2 EUR, dann ändert sich das Delta der Option um 5% der Aktienkursänderung. Also in diesem Fall 5% von 2, was einer Delta-Änderung von 0,1 entspricht.
Die Dezimalschreibweiße ist zwar die mathematisch korrekte Art, das Gamma zu beschreiben aber in der Praxis sagt bzw. schreibt man selten, dass eine Option ein Gamma von 0,05 oder 0,1 hat, sondern man sagt stattdessen, dass eine Option ein Gamma von 5 oder 10 hat.
Ein Gamma von 10 bedeutet somit, dass das Delta einer Call Option um 10 im Wert steigt, wenn das Underlying einen Euro im Wert ansteigt.
💭 Beispiel
Stellt euch eine Aktie vor, die aktuell einen Wert von 50 EUR hat und eine Call Option auf diese Aktie, deren Wert aktuell 5 EUR ist. Das Delta der Option ist in diesem Fall 50 und das Gamma der Option ist 10. D.h. steigt der Wert der Aktie auf 51 EUR oder fällt auf 49 EUR (also die Aktie bewegt sich um genau einen Euro), dann steigt der Kurs der Call Option auf 5,50 EUR (bei steigendem Aktienkurs) oder fällt auf 4,50 EUR (bei fallendem Aktienkurs).
Bei einem Aktienkurs von 51 EUR beträgt das Delta aber nicht mehr 50 sondern, weil das Gamma der Option 10 war und das Underlying um einen Euro gestiegen ist, 60. D.h. steigt der Aktienkurs auf 52 EUR, dann steigt der Kurs der Option von 5,50 EUR auf 6,10 EUR.
Weil sich die Option dadurch aber noch mehr ins Geld bewegt hat, beträgt das Gamma nicht mehr 10 sondern ist auf 5 gefallen. Das heißt ein Anstieg des Underlings von 52 EUR auf 53 EUR, würde das Delta von 60 auf 65 erhöhen.

Ähnlich ist es auch bei einem Aktienkurs von nur noch 49 EUR. Auch hier ist das Delta der Option nicht mehr 50, sondern ist, weil das Gamma der Option in dem Fall 10 ist und das Underlying um einen Euro fällt, auf 40 gefallen. Entsprechend fällt der Kurs der Option von 4,50 EUR auf nur noch 4,10 EUR, wenn der Kurs der Aktie von 49 EUR auf 48 EUR fällt.
Berechnung des Gammas
Um das Gamma einer Option zu berechnen, gibt es grundsätzlich zwei Möglichkeiten. Die korrekte Variante ist, dass man das Gamma mithilfe eines Optionspreismodells berechnet und die weniger komplizierte Variante ist die Berechnung mithilfe von Marktdaten. Ich erkläre euch gleich beide Varianten etwas genauer, allerdings will ich an dieser Stelle auch hinweisen, dass es in aller Regel gar nicht notwendig ist, dass ihr das Gamma einer Option selbst berechnet, weil ihr diese Information auch online auf verschiedenen Webseiten einsehen könnt oder einfach mithilfe meines Optionspreisrechners selbst berechnen könnt bzw. ein guter Broker euch die Information auch immer bereitstellt.
Ich nutze für den Optionshandel zum Beispiel den Broker Estably (bis vor kurzem noch unter „Banx Broker“ bekannt) und dort wird das Gamma als Standardinformation bei jeder Option direkt mit angezeigt. D.h. noch bevor ich überhaupt eine Option kaufe oder verkaufe, erhalte ich alle Informationen direkt von meinem Broker, die ich benötige.
Das Gamma wird bei eurem Broker dabei in der sogenannten Option Chain angezeigt. Dort findet ihr alle Call und Put Optionen geordnet nach dem jeweiligen Strike Preis für eine bestimmte Laufzeit. Neben dem Preis für jede Option werden in der Option Chain aber auch alle Greeks inklusive dem Gamma angezeigt. Hier mal ein Screenshot, wie das ganze bei Estably aussieht.
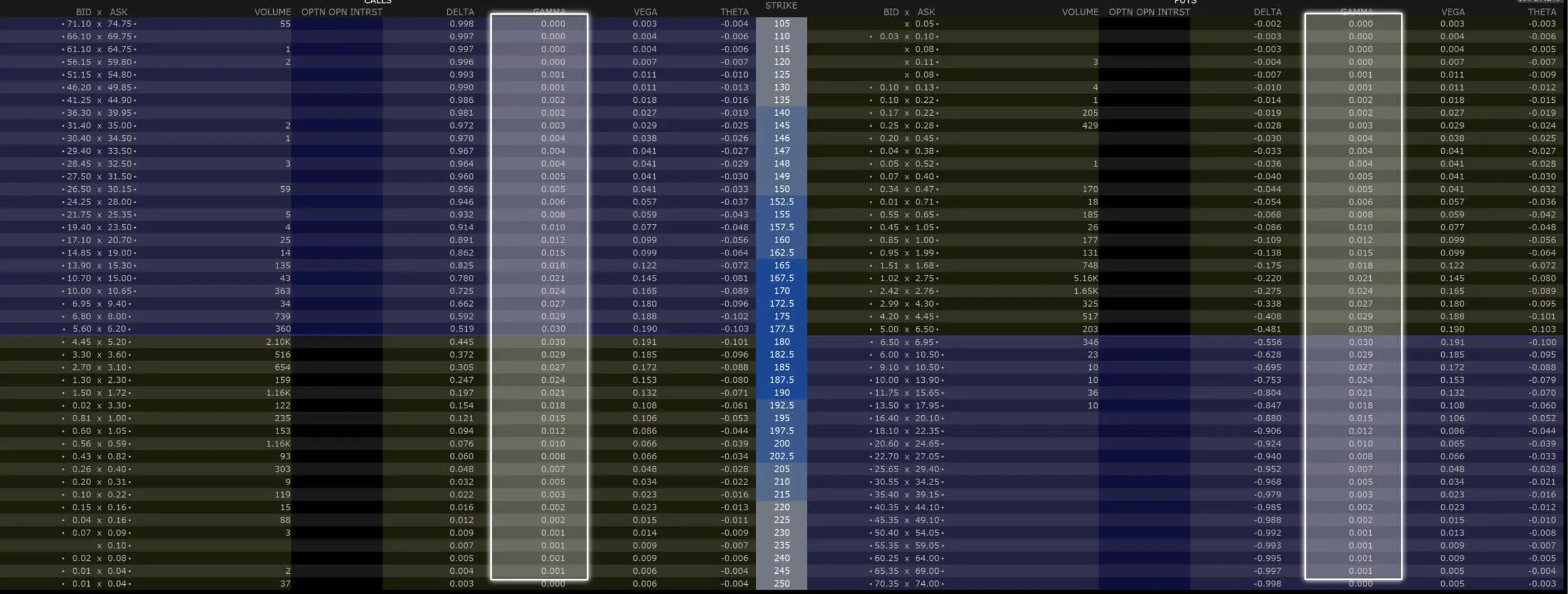
Das Bild zeigt eine beispielhafte Option Chain und welche Informationen darin bereitgestellt werden. Hervorgehoben ist der Bereich, aus dem man das Gamma von Put und Call Optionen sehen kann.
Wenn ihr auch Optionen handeln möchtet, dann kann ich euch Estably wirklich nur empfehlen. Im Hintergrund nutzt Estably Interactive Brokers was ein Tool ist, das auch von Profis genutzt wird. Entsprechend bekommt ihr dort alle Informationen, die für den Optionshandel notwendig sind und könnt euch auch alles so individuell einrichten, wie ihr möchtet.
Wenn ihr ein Depot bei Estably eröffnen wollt, dann könnt ihr das über diesen Link machen*. Das gibt euch Zugriff auf ein wirklich tolles Trading Tool, einen günstigen Broker und ihr unterstützt gleichzeitig noch meine Arbeit, weil ich bei einer Depoteröffnung eine kleine Gebühr von Estably bekomme (ohne, dass das ganze für euch teurer wird).
Aber zurück zum Thema. Auch wenn ihr das Gamma einer Option selbst nicht berechnen müsst, ist es dennoch ganz gut zu wissen, wie es berechnet wird, damit ihr besser verstehen könnt, wie sich das Gamma einer Option verändert je nachdem welche Marktveränderungen eintreten.
Mithilfe eines Optionspreismodells
Grundsätzlich gibt es verschiedene mathematische Modelle zur Preisberechnung von Optionen, allerdings hat sich in der Praxis das sogenannte „Black-Scholes-Modell“ durchgesetzt, dass nach den beiden US-Amerikaner Fischer Black und Myron Scholes benannt wurde, die dieses Modell 1973 veröffentlichten.
🔥 Gut zu wissen
Während das Black-Scholes-Modell nach Fischer Black und Myron Scholes benannt ist, spielte Robert C. Merton eine ebenso entscheidende Rolle in der Entwicklung dieses bahnbrechenden Ansatzes zur Optionspreisbewertung. Merton, der zeitgleich an ähnlichen Gleichungen arbeitete, erweiterte das Modell um eine dynamische Komponente, die es ermöglicht, den zeitlichen Verfall einer Option – später bekannt als Theta – zu berechnen.
Trotz seines wesentlichen Beitrags wird Mertons Name oft übersehen, wenn es um das Black-Scholes Modell geht. Er erhielt jedoch gemeinsam mit Scholes 1997 für ihre bahnbrechende Arbeit den Nobelpreis für Wirtschaftswissenschaften, während Black, der 1995 verstarb, diesen postum nicht erhalten konnte.
Das besondere am Black-Scholes Modell ist, dass es ermöglichte, die Preisberechnung einer Option auf eine mehr oder weniger einfache mathematische Formel herunterzubrechen, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.
Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt.
Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.
Das Gamma ist dabei die zweite Ableitung des Black-Scholes Modells nach dem Preis des Underlyings weswegen das Gamma auch angibt, um wie viel sich das Delta der Option ändert, wenn sich der Wert des Underlyings um 1 erhöht oder verringert.
Die Formel bzw. besser gesagt Formeln für das Black-Scholes Modell sind relativ komplex und ich möchte hier auch nicht zu sehr ins Detail gehen, weswegen ich einfach auf Wikipedia verweisen würde, wenn ihr gern mehr dazu erfahren wollt oder spielt einfach mit meinem Optionspreis-Rechner, wenn ihr ein Gefühl bekommen wollt, wie sich das Gamma einer Option unter verschiedenen Marktbedingungen verändert.
Mithilfe von Marktbeobachtungen
Das Gamma einer Option lässt sich ähnlich wie das Delta aber auch grob grob abschätzen, indem man am Markt die Preise der Option beobachtet und verfolgt, wie sich der Optionspreis bei kleinen Änderungen des Underlyings verändert.
Dazu benötigt man lediglich die Optionspreise zu drei verschiedenen Preisen des Underlyings. Zunächst betrachtet man die ersten beiden Preise des Underlyings und bildet die Differenz zwischen den entsprechenden Optionspreisen. Die Differenz teilt man dann durch die Differenz der beiden Underlying-Preise, um eine ungefähre Annäherung für das Delta für den ersten Preis des Underlyings zu erhalten. Anschließend wiederholt ihr den Vorgang für die letzten beiden Underlying-Preise, um das Delta für den zweiten Preis zu bestimmen.
Das Gamma ergibt sich nun aus der Differenz dieser beiden Delta-Werte, geteilt durch die Differenz der beiden Underlying-Preise, die für das zweite und dritte Delta verwendet wurden. Wie beim Delta sollte man diese Methode auch beim Gamma aber nur bei kleinen Preisänderungen des Underlyings anwenden, da bei zu großen Änderungen die Abweichungen vom tatsächlichen Gamma-Wert zu groß werden könnten. Empfehlenswert sind daher nur Differenzen von maximal einem Euro oder einem Dollar.
Eine andere Interpretation des Gammas
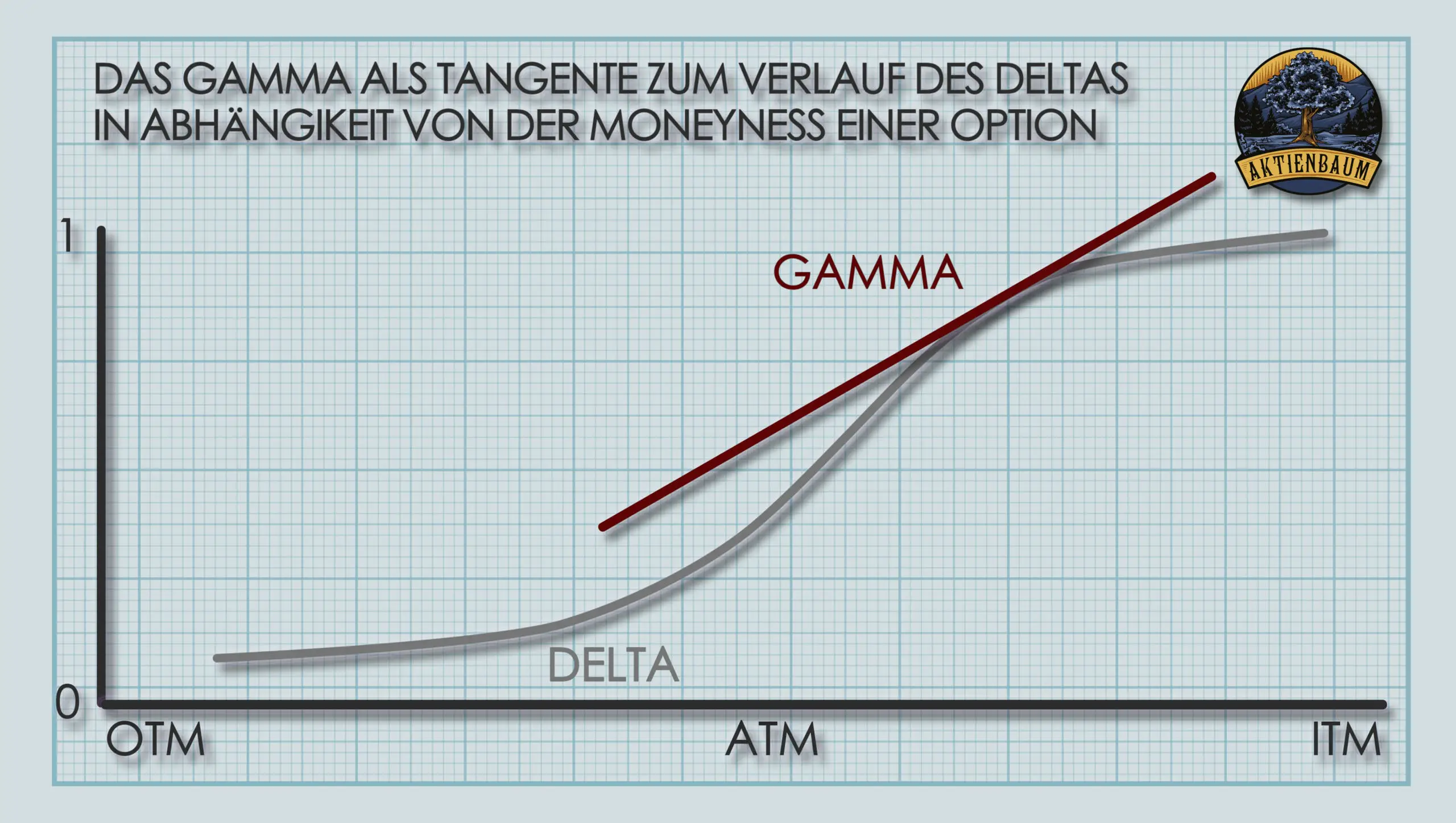
Das Gamma kann aber auch grafisch interpretiert werden, wenn man sich dazu den typischen Verlauf des Deltas einer Option in Abhängigkeit vom Kurs anschaut, wie ich es euch in der unteren Grafik anhand einer Call Option zeige.
Legt man an die Grafik eine Tangente an, also eine Linie, die die Grafik in nur einen Punkt schneidet, dann sagt der Anstieg dieser Tangente aus, wie sehr sich der Wert des Deltas verändert, wenn sich der Wert des Underlyings leicht erhöht oder verringert.
Das ist auch genau die Definition des Gammas, weswegen der Anstieg der Tangente somit auch dem Gamma der Option entspricht. Bewegt sich die Option immer mehr ins Geld hinein, dann ist der Anstieg der Tange auch immer größer bzw. nähert er sich immer mehr 1 an, genau wie wir oben auch schon beim Gamma gesehen haben.
Fällt der Wert des Underlyings aber, dann verringert sich der Anstieg der Tangente immer mehr und nähert sich null an, wie es auch bei dem Gamma der Fall ist.
Weiter oben habe ich euch schon gesagt, dass das Gamma nichts anderes ist als die zweite Ableitung der Black-Scholes Formel nach dem Preis ist und grafisch betrachtet, ist das auch die selbe Definition der Tangente.
Der Zusammenhang des Delta mit anderen Markteinflüssen
Moneyness der Option
Das Gamma einer Option ist nicht konstant und ändert sich basierend auf den aktuellen Marktgegebenheit. Den größten Einfluss auf das Gamma hat dabei der Preis des Underlyings bzw. die sogenannte „Moneyness“ der Option.
🔥 Gut zu wissen
Die „Moneyness“ einer Option gibt an, wie nah der Strikepreis der Option am aktuellen Marktpreis des Underlyings liegt. Für Call Optionen gibt es drei Moneyness-Zustände, die eine Option haben kann (bei Put ebenso, allerdings ist die Beziehung zwischen Marktpreis und Strikepreis genau entgegengesetzt):
- Im Geld (In the Money – ITM): wenn der aktuelle Marktpreis über dem Strikepreis liegt
- Am Geld (At the Money – ATM): wenn der aktuelle Marktpreis nahe am Strikepreis liegt
- Aus dem Geld (Out of the Money – OTM): wenn der aktuelle Marktpreis unter dem Strikepreis liegt
Die Grafik unten zeigt den Verlauf des Deltas (graue Linie) und des Gammas (grüne Linie) in Abhängigkeit von der Preisänderung des Underlyings bzw. der Moneyness einer Call Option.
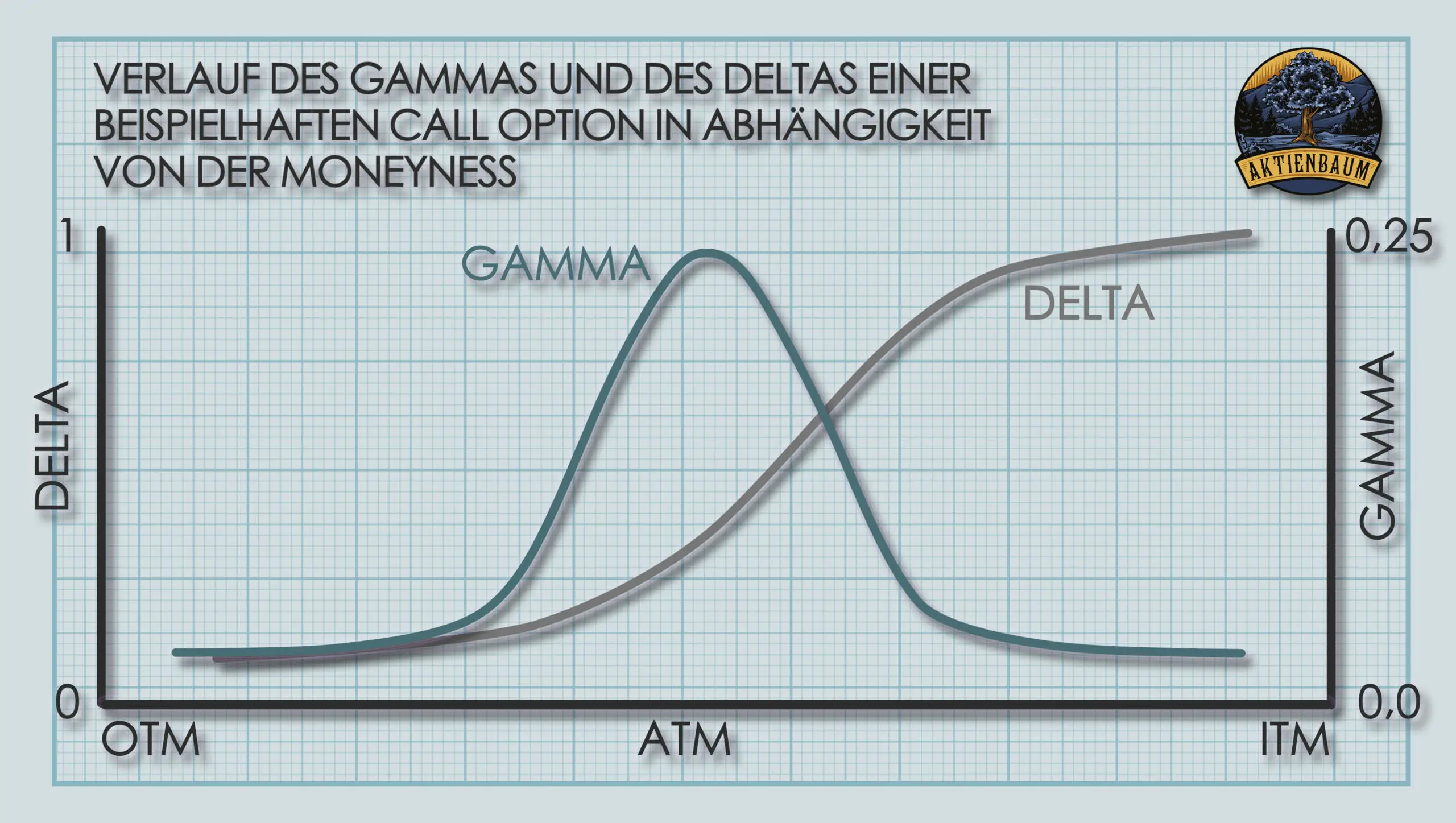
Die Grafik zeigt dabei deutlich, dass das Gamma dann am höchsten ist, wenn sich die Option am Geld (ATM) befindet. Das führt dazu, dass am Geld bereits sehr kleine Änderungen des Kurses des Underlyings schon einen erheblichen Einfluss auf das Delta haben.
Im Gegensatz dazu ist das Gamma einer Option fast null, wenn sich die Option tief im oder außerhalb des Geldes befindet. Das bedeutet im Umkehrschluss aber auch, dass sich das Delta einer Option, die sich tief im oder außerhalb des Geldes befindet ebenfalls so gut wie nicht ändert bei kleinen Preisänderungen des Underlyings.
Restlaufzeit
Ein anderer wichtiger Einflussfaktor auf das Gamma ist die Restlaufzeit der Option. Nimmt die Restlaufzeit der Option ab, steigt das Gamma einer Option tendenziell.
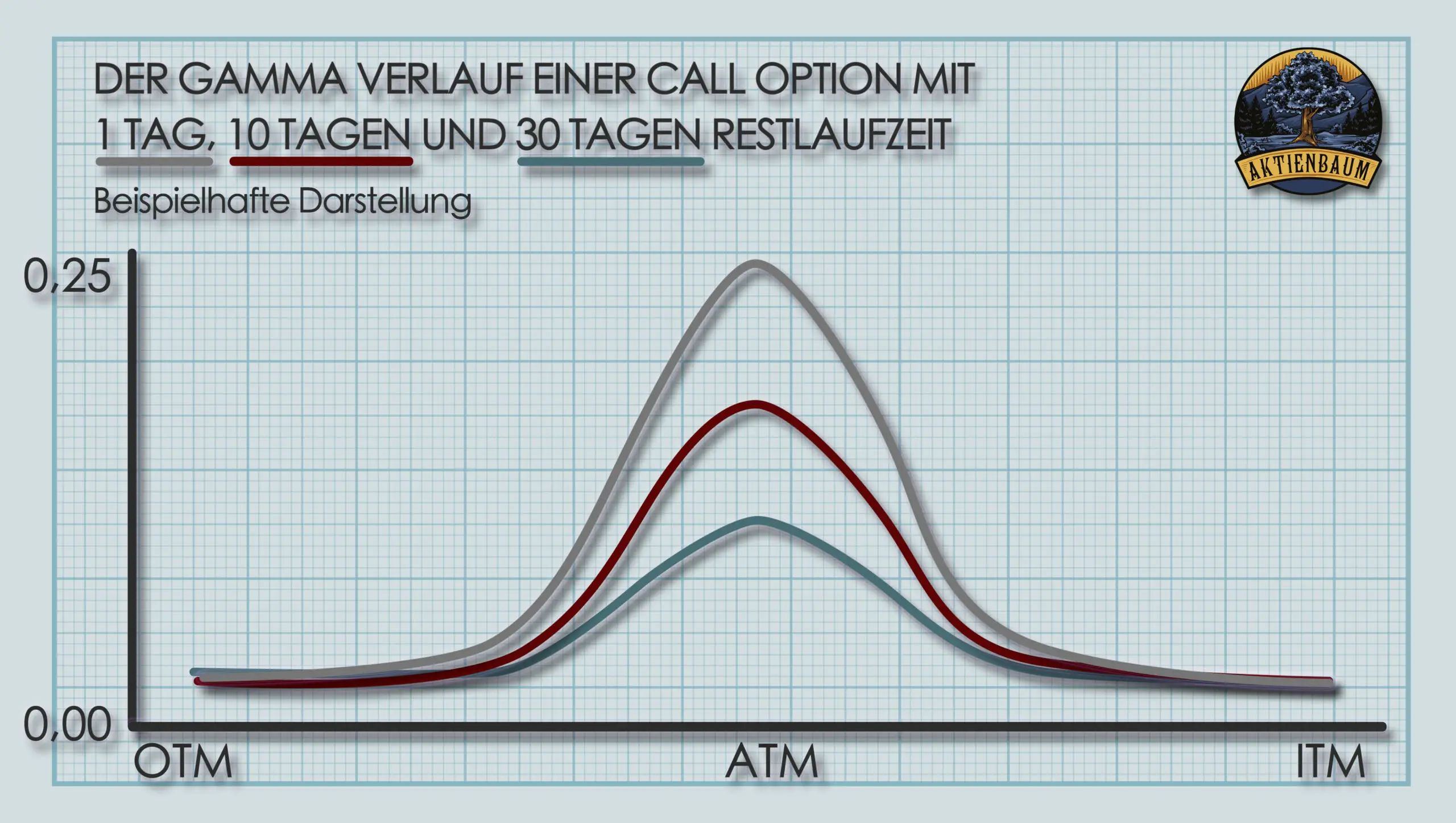
Das ist für viele Optionsverkäufer auch der Grund, warum sie Optionen nie bis Laufzeitende halten, sondern schon mehrere Tage vorher zurückkaufen trotz der zusätzlichen Handelsgebühren.
Würde man seine Optionen nämlich bis Laufzeitende halten, würde das Gamma der Option wenige Tage vor Fälligkeit so groß werden, dass bereits kleine Änderungen des Preises des Underlyings einen erheblichen Einfluss auf das Gamma und damit das Delta haben und der Optionspreis sich schnell verändern kann. Wenn ihr gern mehr darüber erfahren wollt, wann man Optionen wieder zurückkaufen sollte, dann lest euch doch am besten diesen Artikel von mir durch.
Volatilität
Das Gamma ist aber auch sehr stark von der Volatilität einer Option abhängig. Befindet sich eine Option am Geld, dann ist das Gamma dieser Option höher, je niedriger die implizite Volatilität des Underlyings ist. Befindet sich eine Option aber im oder außerhalb des Geldes, dann ist die Beziehung zwischen Gamma und Volatilität genau umgekehrt.
Bei Optionen, die sich im oder außerhalb des Geldes befinden, ist das Gamma umso höher, je höher die implizite Volatilität des Underlyings ist. Den Zusammenhang könnt ihr sehr gut in der folgenden Grafik sehen.
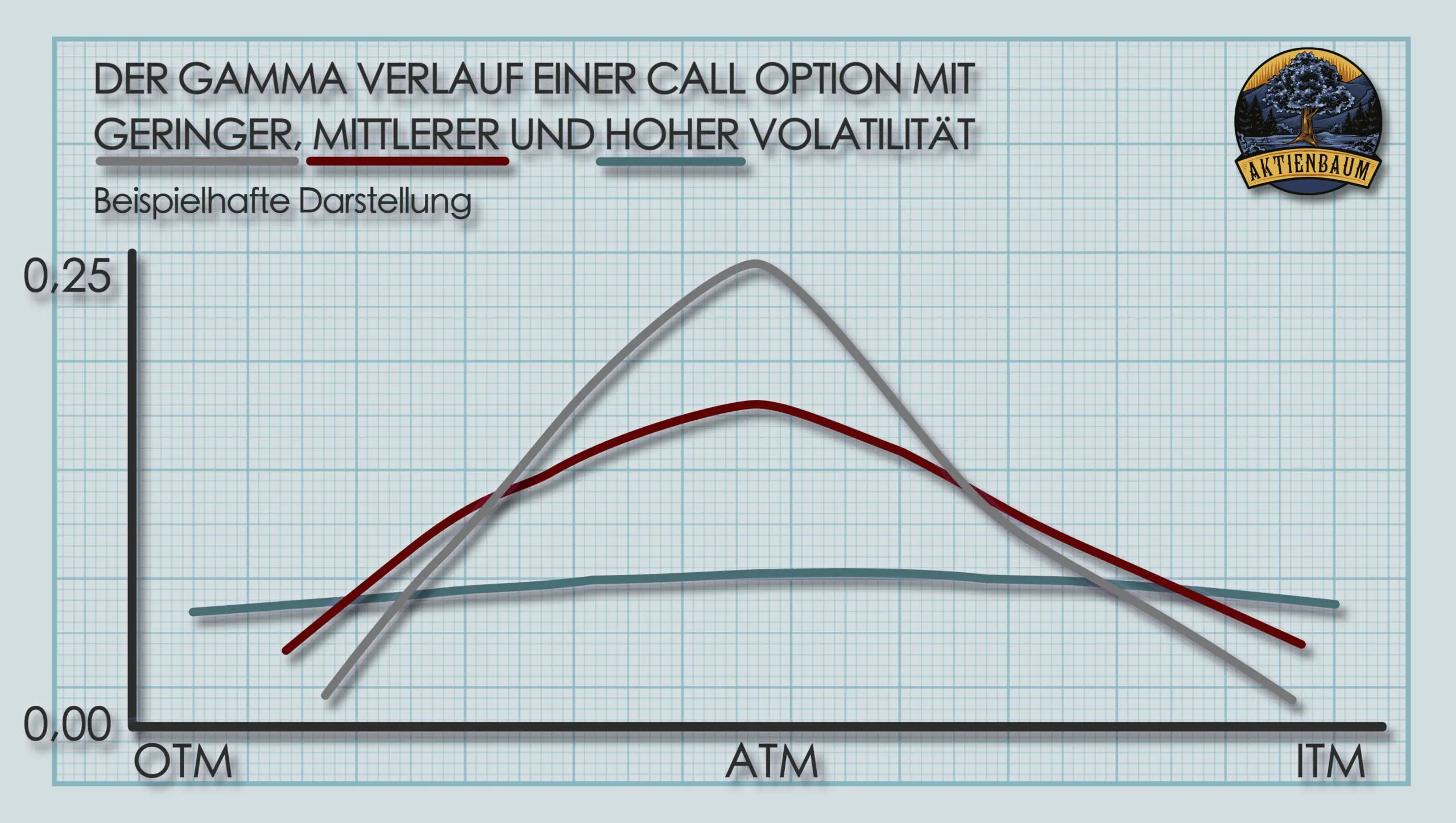
Die Abhängigkeit des Gammas von der Volatilität macht intuitiv aber auch Sinn, wenn man sich das Zusammenspiel von Volatilität und Delta noch einmal vor Augen führt.
Stellt euch dafür einfach eine Option mit geringer Volatilität des Underlyings vor. Aufgrund der geringen Vola, hat die Optionen auch nur einen geringen Zeitwert und aufgrund des geringen Zeitwerts steigt das das Delta der Option schnell an, je mehr sich die Option ins Geld bewegt. Genau dieser schnelle Anstieg des Deltas bedeutet ja, dass das Gamma entsprechend auch sehr hoch sein muss.
Der Anstieg des Deltas ist somit also höher als bei Optionen, deren Underlyings eine hohe implizite Volatilität haben.
Als allgemeine Faustregel gilt, dass das Gamma einer Option umso konstanter ist, je höher die Volatilität des Underlyings ist. Bei niedriger Volatilität des Underlyings ist das Gamma am Geld am höchsten und fällt ab, je tiefer sich die Option ins Geld oder aus dem Geld heraus bewegt.
Diese Faustregel ist besonders interessant, wenn man eine Delta-neutrale Position haben möchte. Mehr dazu erkläre ich euch in meinem Artikel zum Thema „Delta Hedging“.
* Das ist ein Werbe- oder Affiliate-Link. Wenn du über diesen Link einkaufst oder einen Vertrag abschließt, bekommen wir von einigen Anbietern eine Vergütung. Für dich ändert sich dabei nichts am Preis. Mit deinem Klick unterstützt du unser Projekt. Herzlichen Dank für deine Unterstützung!

