Was sagen die Griechen über eine Option aus?

Wenn man sich dazu entscheidet mit Optionen zu handeln oder sich einfach nur erst einmal mit dem Thema Optionshandel beschäftigen möchte, dann führt kein Weg an den sogenannten Griechen oder auch Greeks vorbei. Ich bemerke dabei aber immer wieder, dass die Griechen für viele Privatinvestoren ein wenig zu mathematisch und schwer verständlich sind. Dabei sind die Greeks viel einfacher zu verstehen als man denkt und wenn man sie beherrscht auch eine wahre Hilfe im Optionshandel.

Die Griechen bzw. Greeks einer Option sind Sensitivitätskennzahlen. D.h. sie geben an, um wie viel sich der Preis einer Option ändert bzw. wie sensitiv die Option auf die Änderung reagiert, wenn sich ein einzelner Einflussfaktor um einen bestimmten Wert verändert.

Rein mathematisch betrachtet, gibt es unendlich viele Griechen einer Option, weil jeder der Greeks selbst auch wieder einen Greek hat (dazu später mehr) allerdings hat das im täglichen Optionshandel keinen Einfluss, weswegen man sich nur auf die wichtigsten Griechen konzentrieren sollte. 

Dieser Artikel setzt übrigens voraus, dass ihr schon verstanden habt was Optionen sind und wie sie funktionieren. Solltet ihr dazu noch einige Wissenslücken haben, dann solltet ihr vielleicht zuerst meinen Grundlagenartikel über Optionen durchlesen.

Warum heißen die Greeks eigentlich so?

Ich bin ein großer Fan von Details und Hintergrundwissen, da es meist hilft ein Thema besser zu verstehen. Deswegen würde ich zunächst gern einmal erklären, wie die Griechen eigentlich zu ihrem Namen gekommen sind da es für das Gesamtverständnis wirklich sehr hilfreich ist. 

Wer sich dafür aber überhaupt nicht interessiert und stattdessen direkt mehr über die einzelnen Griechen erfahren möchte, der kann diesen Teil überspringen und direkt mit dem Kapital „Was für Griechen gibt es“ weitermachen.

Dank unserer modernen Computer ist die Berechnung eines fairen Preises für eine Option extrem einfach und schnell geworden, aber das war nicht immer so.

Bis 1973 hat es noch Stunden gedauert, um die bis zum damaligen Zeitpunkt vorherrschenden Preismodelle zur Bestimmung eines Optionswerts durchzurechnen.

Das alles änderte sich aber als 1973 die beiden US-Amerikaner Fischer Black und Myron Scholes ein neues Modell entwickelten, dass es ermöglichte, schnell und einfach den fairen Wert einer Option zu bestimmen. Das später als „Black-Scholes-Modell“ getaufte Optionspreismodell konnte auf eine mehr oder weniger einfache mathematische Formel heruntergebrochen werden, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.

Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt. 

Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.

Was für Griechen gibt es?

Delta

Das Delta einer Option gibt an, um wie viel sich der Preis der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt. D.h. bei einem Delta von 0,3 würde der Wert der Option um 0,3 EUR zunehmen, wenn der Wert des Underlyings um einen Euro steigt.

Das Delta gilt als eine der wichtigsten Risikokennzahlen bei Optionen, weil es den direkten Einfluss von Preisbewegungen zeigt. Der Wert des Deltas kann immer nur zwischen -1 und +1 liegen wobei für Calls und Puts immer gilt:

• Bei Calls ist das Delta der Option immer zwischen 0 bis 1 
• Bei Puts ist das Delta der Option immer zwischen -1 bis 0

Rein mathematisch betrachtet ist das Delta die erste Ableitung des Optionspreises nach dem Preis des Underlyings im verwendeten Optionspreismodell. 

In der Grafik unten kann man schön erkennen, dass das Delta somit der Anstieg der Tangente der Optionspreiskurve ist. Bitte entschuldigt noch einmal, dass es manchmal hier so mathematisch wird aber die einen von euch bevorzugen vielleicht lieber die textliche Erklärung und die anderen die eher mathematische Erklärung.

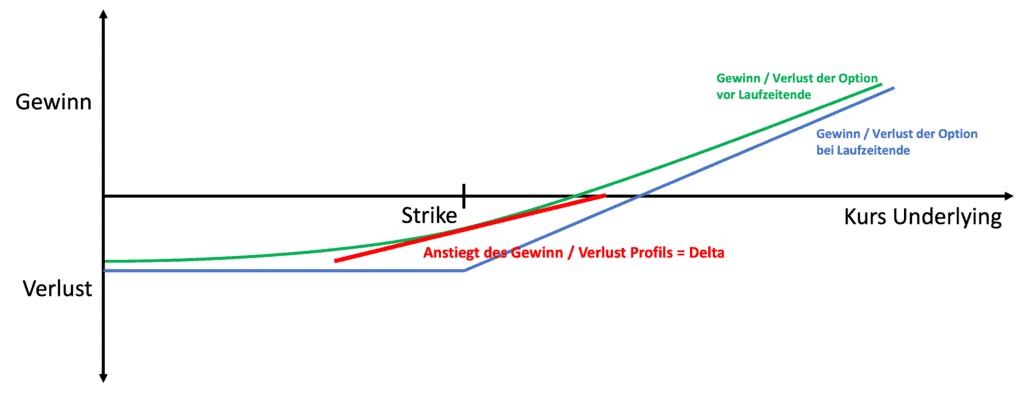
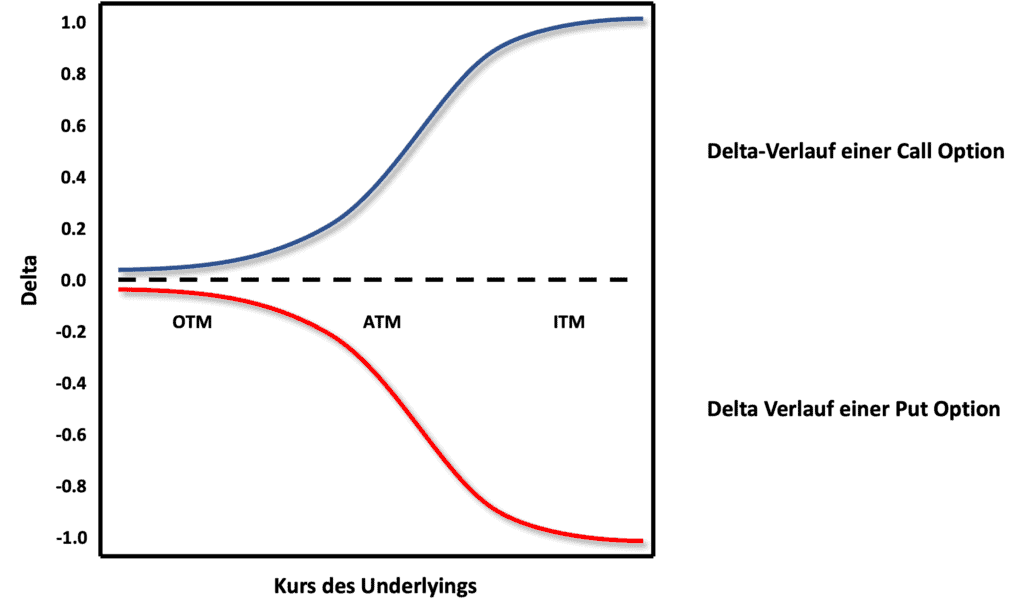
Umso mehr man sich also in das Geld (ITM) einer Option bewegt, desto steiler wird die Tangente bzw. desto größer wird das Delta. Weiter außerhalb des Geldes (OTM), wird die Tangente flacher bzw. das Delta der Option kleiner. Am Geld (ATM) ist das Delta einer Option immer grob 0,5. 

D.h. aber also, dass weit außerhalb des Geldes befindliche Option mit ihrem Delta von fast null sich so gut wie nicht mit dem Kurs des Underlyings bewegen und weit im Geld befindliche Optionen mit ihrem Delta von fast 1 bzw. -1 sich fast genauso wie der Kurs des Underlyings verändern.

Das Delta einer Option verändert sich mit kürzer werdender Restlaufzeit und wird im ITM Bereich immer größer und im OTM Bereich immer kleiner je weniger Tage bis zum Laufzeitende der Option verbleiben (unter der Annahme, dass alle anderen Faktoren gleichbleiben und sich der Preis des Underlyings quasi nicht von der Stelle bewegt). 

Grafisch könnt ihr das im Bild unten sehen. Umso näher man sich an das Laufzeitende einer Option bewegt, desto mehr nähert sich der theoretische Optionspreisverlauf dem finalen Auszahlungsprofil der Option an.

D.h. dass die Optionspreiskurve kurz vor Laufzeitende im ITM Bereich immer steiler wird (also das Delta sich immer mehr an 1 bzw. -1 annähert) und im OTM Bereich immer flacher (also das Delta sich immer mehr der Null annähert) wird.

Viele Optionshändler nutzen das Delta auch als grobe Faustformel, um auszurechnen, wie wahrscheinlich es ist, dass eine Option bei Laufzeitende im Geld liegt. Ein Delta von 0,6 oder -0,6 bedeutet dabei, dass die Option mit 60%-iger Wahrscheinlichkeit bei Laufzeitende im Geld liegt. 

Ich selbst bin aber nur ein sehr bedingter Fan von dieser Regel. Ja, umso größer das Delta ist, desto höher ist die Wahrscheinlichkeit, dass eine Option am Ende im Geld landet bzw. umso niedriger das Delta, desto niedriger ist die Wahrscheinlichkeit.

Allerdings würde ich das Delta nie eins zu ein in eine Wahrscheinlichkeit umwandeln, um darauf meine Entscheidungen zu treffen. Mein Ziel im Optionshandel ist es u.a. ja, dass ich Option besonders dann verkaufe, wenn ich der Meinung bin, dass der Preistrend des Underlyings sich mit sehr hoher Wahrscheinlichkeit umkehrt und ich somit die Option schnell wieder günstig zurückkaufen kann.

D.h. auch wenn das Delta 0,8 sein sollte (und damit die angebliche Wahrscheinlichkeit, dass die Option bei Laufzeitende im Geld landet, bei 80% liegt) ist meine persönliche Wahrscheinlichkeit für den Ausgang der Option eine ganz andere. 

Also benutzt diese Faustregel bitte mit Vorsicht und macht euch selbst einen Kopf, wohin der Preis des Underlyings sich sehr wahrscheinlich bewegen wird.

Wenn ihr noch mehr Details zum Delta einer Option erfahren wollt, dann solltet ihr euch unbedingt meinen Detail-Artikel zum Delta von Optionen anschauen.

Gamma

Das Gamma einer Option gibt an, um wieviel sich das Delta der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt. D.h. bei einem Delta von 0,3 und einem Gamma von 0,1 würde das Delta der Option um 0,1 auf 0,4 steigen, wenn sich der Wert des Underlyings um einen Euro erhöht.

Das Gamma einer Option kann dabei zwischen 0 und 1 liegen und da es sich um einen absoluten Wert handelt, gibt es auch keinen Unterschied bei Puts und Calls. D.h. ein Gamma von 0,1 erhöht immer das Delta einer Option um 0,1 bei einem Preisanstieg des Underlyings um eine Währungseinheit ganz egal ob Put oder Call oder Long oder Short.

Unter identischen Rahmenbedingungen, d.h. bei gleichem Strike-Preis, gleichem Underlying Kurs, gleicher Laufzeit, gleichem Zinssatz usw., ist das Gamma eines Calls und eines Puts sogar identisch.

Mathematisch betrachtet ist das Gamma die zweite Ableitung des Optionspreises nach dem Preis des Underlyings im verwendeten Optionspreismodell (bzw. auch die erste Ableitung des Deltas nach dem Preis des Underlyings, aber jetzt wird es echt nerdig weswegen ich es damit gut sein lassen will).

Die Grafik unten zeigt den Verlauf des Deltas (blaue Linie) und des Gammas (rote Linie) in Abhängigkeit von der Preisänderung des Underlyings für eine Call Option. Wer wieder einen mathematisch-grafischen Vergleich haben will, der kann sich das Gamma als den Anstieg der Tangente des Deltas vorstellen.

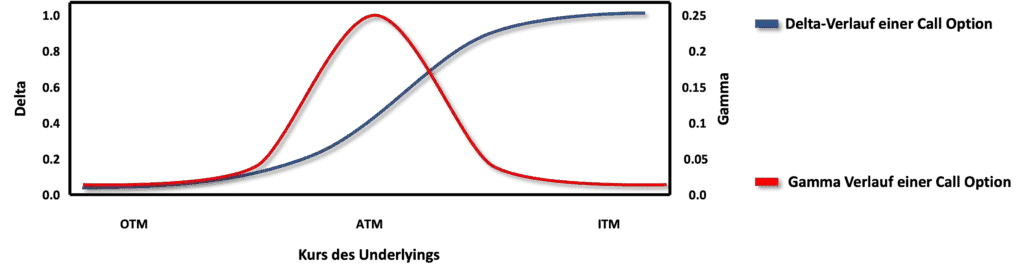
Die Grafik zeigt dabei deutlich, dass das Gamma dann am höchsten ist, wenn sich die Option am Geld (ATM) befindet. Das führt dazu, dass am Geld bereits sehr kleine Änderungen des Kurses des Underlyings schon einen erheblichen Einfluss auf das Delta haben. 

In letzter Zeit hört man immer wieder von einem Gamma Squeeze, der Aktienkurse schnell in die Höhe treibt. Was ist das aber eigentlich und wie entsteht so ein Squeeze? Falls es euch interessiert, lest euch einfach meinen Artikel hier dazu durch.

Ein anderer wichtiger Einflussfaktor auf das Gamma ist die Restlaufzeit der Option. Nimmt die Restlaufzeit der Option ab, steigt das Gamma einer Option tendenziell.

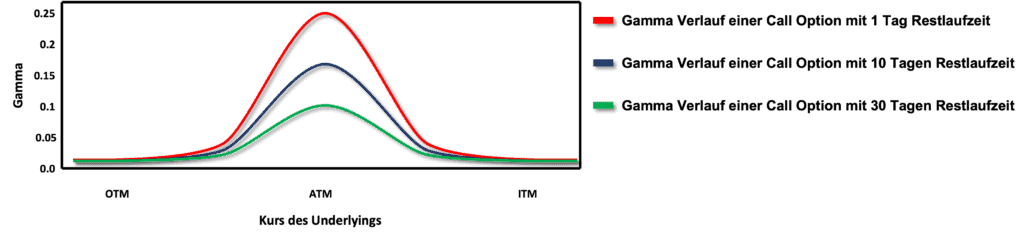
Das ist für viele Optionsverkäufer auch der Grund, warum sie Optionen nie bis Laufzeitende halten, sondern schon mehrere Tage vorher zurückkaufen trotz der zusätzlichen Handelsgebühren. 

Würde man seine Optionen nämlich bis Laufzeitende halten, würde das Gamma der Option wenige Tage vor Fälligkeit so groß werden, dass bereits kleine Änderungen des Preises des Underlyings einen erheblichen Einfluss auf das Gamma und damit das Delta haben und der Optionspreis sich schnell verändern kann.

Wenn ihr noch mehr Details zum Gamma einer Option erfahren wollt, dann solltet ihr euch unbedingt meinen Detail-Artikel zum Gamma von Optionen anschauen.

Theta

Das Theta einer Option gibt an, um wieviel sich der Preis der Option jeden Tag verringert. Dieser Wert ist immer negativ und wird mit immer kürzer werdender Restlaufzeit der Option größer. Hat eine USD Option ein Theta von -2, dann bedeutet dass, dass der Wert der Option morgen bei sonst gleichbleibenden Bedingungen 2 USD weniger wert sein wird. 

Man spricht hierbei auch vom Zeitwertverfall einer Option aber gerade Anfängern im Optionshandel ist dieses Prinzip nicht immer gleich ein Begriff, deswegen noch eine kurze Erklärung zum Zeitwertverfall. Für diejenigen unter euch, die damit direkt etwas anfangen können wieder der Hinweis, einfach den nächsten Absatz zu überspringen.

Optionen besitzen einen inneren Wert und einen Zeitwert. Der innere Wert, ist der Wert, den die Option bei aktuellem Preis des Underlyings zum Laufzeitende auszahlen würde und der Zeitwert ist der Wert, den die Option zusätzlich noch besitzt, weil es eine Wahrscheinlichkeit gibt, dass der innere Wert noch steigen könnte. Das klingt jetzt komplizierter als es eigentlich ist, deswegen eine kleine Grafik, um das ganze deutlicher zu machen.

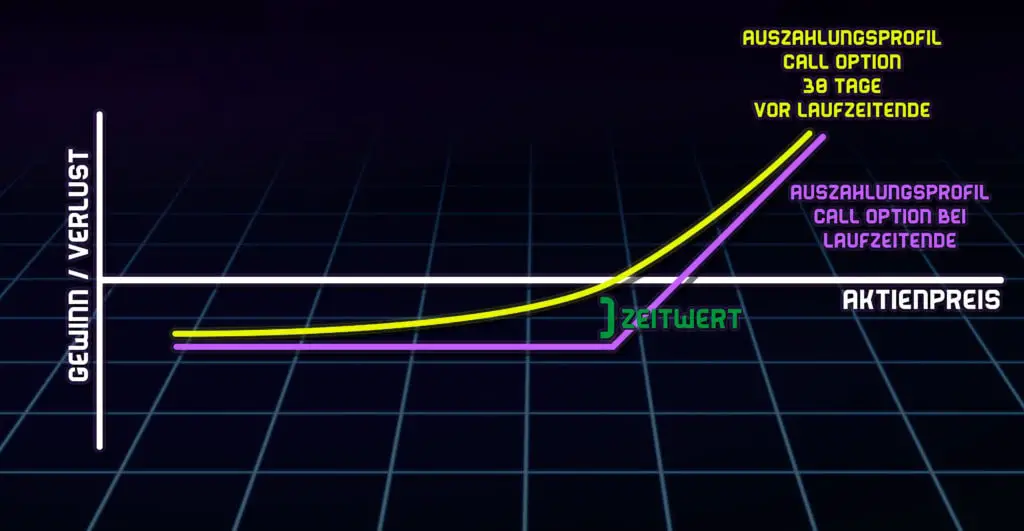
In der Grafik kann man gut sehen, wie das Auszahlungsprofil der Option bei Laufzeitende ist (lila Linie). Der aktuelle Wert liegt aber immer mal mehr oder mal weniger darüber und dieser zusätzliche Wert ist der Zeitwert der Option. Das Theta der Option gibt nun also an, um wie viel dieser Zeitwert täglich abnimmt. 

Besonders sichtbar ist der Zeitwert bei Optionen, die sich außerhalb des Geldes befinden. Diese Optionen haben keinen inneren Wert (deswegen sind sie ja per Definition außerhalb des Geldes) aber dennoch kann man sie nicht kostenlos am Markt kaufen. 

Je nachdem wie weit sie außerhalb sind (und wie hoch die Volatilität ist) kosten solche Optionen dennoch einige Euro und genau dieser Wert ist der Zeitwert der Option.

Das Theta ist dabei immer negativ, da es aus Sicht des Käufers einer Option angegeben wird. D.h. wenn ihr eine Apple Option kauft und deren Theta momentan -3 beträgt, dann wird der Wert der Option morgen 3 USD weniger betragen (zumindest sofern alle anderen Faktoren, also Preis des Underlyings, Zins, Volatilität usw., gleichbleiben). 

Für den Verkäufer einer Option ist der Zeitwertverfall jedoch ein Gewinn, da dessen Option, die er verkauft an, täglich an Wert verliert und er sie somit günstiger zurückkaufen kann.

Das erklärt auch, warum das Geschäft mit dem Verkauf von Optionen so lukrativ sein kann. Stellt euch vor ihr habt einen Put auf Apple verkauft. Ihr würdet also dann einen Gewinn machen, wenn die Apple Aktie bei Laufzeitende entweder gestiegen oder zumindest auf demselben Preisniveau geblieben ist. 

Allerdings könnt ihr auch dann noch Gewinn machen, wenn die Apple Aktie gefallen ist. Nämlich dann, wenn der Preis der Aktie weniger gefallen ist als die Option an Zeitwert verloren hat. 

Auch hier der Hinweis für die Mathematiker unter euch, dass das Theta die erste Ableitung des Optionspreises nach der Restlaufzeit im verwendeten Optionspreismodell ist.

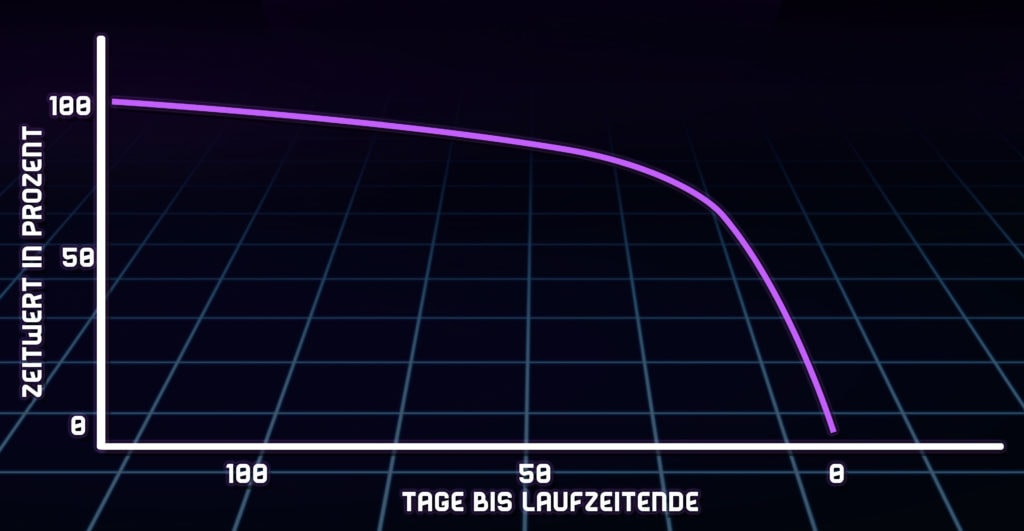
Da das Theta mit kürzer werdender Restlaufzeit zunimmt, verliert eine Option am Ende ihrer Laufzeit immer am meisten an Wert pro Tag. Dabei sei zu erwähnen, dass Optionen, die sich am Geld befinden, immer den größten Zeitwert besitzen und dementsprechend auch das größte Theta. 

Optionen, die sich ganz weit im oder außerhalb des Geldes befinden, haben immer einen sehr geringen Zeitwert und entsprechend auch ein Theta von fast null.

Wenn ihr noch mehr Details zum Theta einer Option erfahren wollt, dann solltet ihr euch unbedingt meinen Detail-Artikel zum Theta von Optionen anschauen.

Vega

Das Vega einer Option gibt an, um wie viel sich der Preis der Option ändert, wenn die Volatilität des Underlyings um einen Prozentpunkt steigt oder fällt. D.h. bei einem Vega von 0,1 würde der Wert der Option um 0,1 EUR steigen, wenn sich die Volatilität des Underlyings um einen Prozentpunkt erhöht.

Wenn ihr euch jetzt wundert, warum ich explizit Prozentpunkt schreibe und nicht Prozent, dann lasst euch kurz den Unterschied erklären.

Wenn ich einen Anfangswert von 50% habe und dieser steigt um 10 Prozent, dann beträgt dieser Wert nun 55%. Wenn derselbe Wert allerdings um 10 Prozentpunkte steigt, dann beträgt er nun 60%. 

Ein Prozentpunkt ist also die absolute Änderung des anfänglichen Prozentwerts und Prozent beschreibt die prozentuale Änderung des Prozentwerts. Wenn die Volatilität also von 13% um 3 Prozentpunkte steigt, dann beträgt sie danach 16%. Dieser kleine, aber feine Unterschied ist extrem wichtig, um das Prinzip des Vegas zu verstehen.

Meiner Meinung nach ist das Vega immer der am schwierigsten zu verstehende Grieche von allen Sensitivitätskennzahlen. Nicht unbedingt, weil die Definition nicht einfach wäre, sondern weil die meisten Leute mit dem Begriff der Volatilität nicht viel anfangen können bzw. zwar ein grobes Verständnis davon haben aber nicht wissen, welche Volatilität beim Vega relevant ist.

Das Thema Volatilität erklären, würde aber definitiv den Rahmen dieses Artikels sprengen, weswegen ich dazu noch einmal einen einzelnen Artikel schreiben werden. An dieser Stelle sei nur so viel gesagt, dass für das Vega einer Option immer die implizite Volatilität relevant ist, und zwar diese, die die Volatilität bis Laufzeitende der Option beschreibt.

Viele fragen sich an dieser Stelle, warum die Laufzeit der Option eine Rolle bei der Volatilität spielt, weil das Underlying kann doch nur eine Volatilität haben aber genau das ist nicht der Fall. Stattdessen hat jede Option bei jeder Laufzeit eine andere Volatilität. 

Nehmen wir einfach an das Underlying hat eine Tages-Vola von 1%, dann müsste die Jahres-Volatilität rein mathematisch betrachtet circa 16% betragen (für die Mathematiker unter euch: ich habe mit 250 Tagen gerechnet). In der Realität weicht die Jahres-Volatilität aber von dieses 16% ab.

Und das macht auch rein intuitiv viel Sinn, denn eine Aktie kann auf Tagesbasis zum Beispiel sehr stark schwanken aber sich auf Jahresbasis nur wenig von der Stelle bewegen. Entsprechend müsst ihr beim Vega immer darauf achten, die richtige Volatilität zu verwenden. 

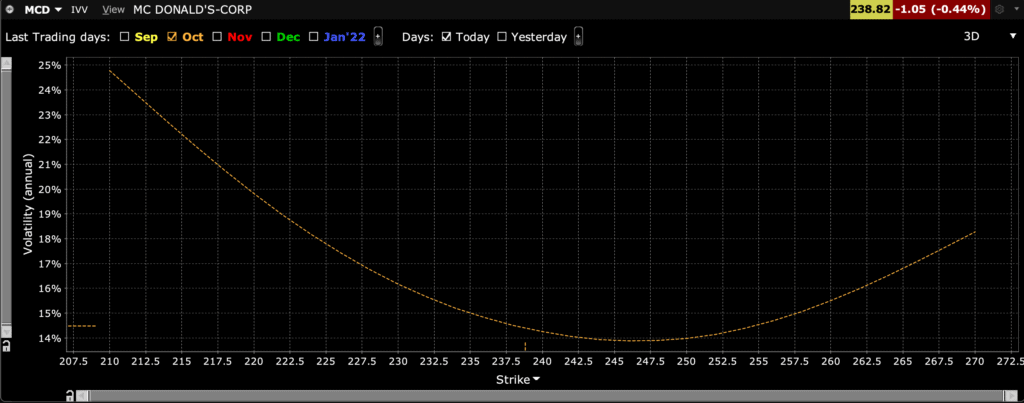
Ein guter Broker sollte euch allerdings aber auch immer die richtige Volatilität zu eurer Option anzeigen können. Ich benutze selbst Banx Broker (die wiederum Interactive Broker im Hintergrund verwenden) und ich kann mir dort alle Volatilitäten zu den jeweiligen Zeithorizonten ganz einfach ziehen wie ihr an folgendem Bild sehen könnt.

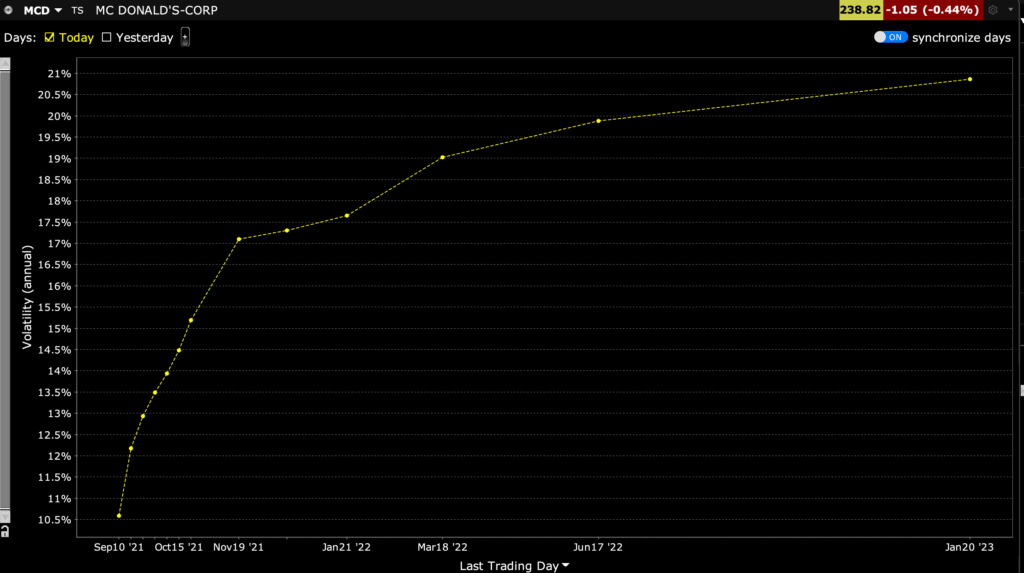
Die Restlaufzeit der Option ist aber nicht der einzige Parameter, der die zu verwendende Volatilität einer Option beeinflussen kann. Ein wichtiger anderer Einflussfaktor ist der Strike-Preis der Option. 

Auch hier haben Anfänger im Optionshandel immer wieder Probleme zu verstehen, dass bei gleichbleibender Laufzeit einer Option die implizite Volatilität einer Option anders ist, je nachdem welchen Strike (bzw. ob man sich im, am oder aus dem Geld befindet) man betrachtet. 

Umso mehr man sich nämlich am Geld befindet desto geringer ist die implizite Volatilität in der Regel und desto mehr man sich aus oder im Geld befindet, desto höher ist die implizite Volatilität in der Regel. Wie ihr unten sehen könnt, sieht das ganze grafisch betrachtet ein wenig wie ein Lächeln aus und im Englischen spricht man dabei vom „Volatility Skew“ (Mehr darüber könnt ihr in meinem Artikel über das Volatility Skew erfahren).

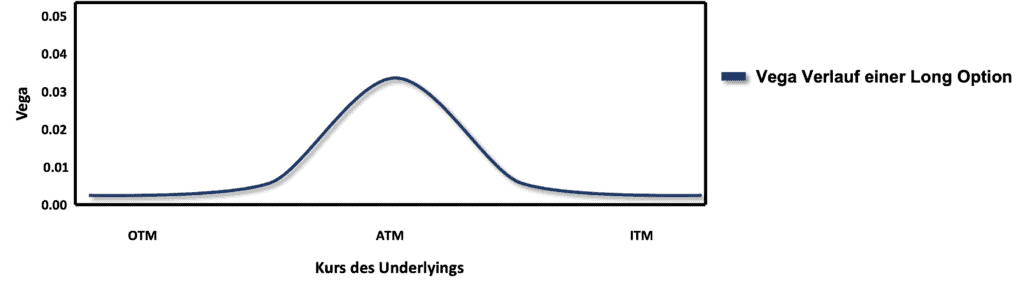
Die Tatsache, ob man sich im, am oder aus dem Geld befindet, hat aber nicht nur Einfluss auf die Volatilität, sondern auch auf das Vega selbst. Während am Geld die Volatilität zwar tendenziell geringer ist als im oder aus dem Geld, so ist das Vega doch im Geld am höchsten und nimmt ab, sobald man sich aus oder in das Geld bewegt.

Als Optionshändler bedeutet das für dich also, dass Schwankungen der Volatilität dann am meisten Einfluss auf den Wert der Option haben, wenn man sich am Geld befindet. Im Geld oder aus dem Geld ist die Wirkung des Vegas tendenziell geringer.

Anders als zum Beispiel das Gamma oder das Theta einer Option unterscheidet sich das Vega je nachdem ob man Käufer oder Verkäufer der Option ist. Es gilt dabei immer

• Long Calls und Puts haben ein positives Vega.
• Short Calls und Puts haben ein negatives Vega.

Dieser Zusammenhang bedeutet für dich als Händler, dass ein Optionskäufer es bevorzugt, wenn die Volatilität zum Kaufzeitpunkt niedrig ist und dann steigt, während ein Optionsverkäufer es bevorzugt, wenn die Volatilität zum Verkaufszeitpunkt hoch ist und dann fällt.

Kleiner Fun Fact zum Vega. Vega ist gar kein griechischer Buchstabe, sondern nur eine Wortneuschöpfung aus dem lateinischen, damit es ähnlich klingt wie die anderen Griechen. 

Wenn ihr noch mehr Details zum Vega einer Option erfahren wollt, dann solltet ihr euch unbedingt meinen Detail-Artikel zum Vega von Optionen anschauen.

Rho

Das Rho einer Option gibt an, um wie viel sich der Preis der Option ändert, wenn sich der risikofreie Zinssatz um einen Prozentpunkt ändert. D.h. bei einem Rho von 0,2 würde der Wert der Option um 0,2 steigen, wenn sich der risikofreie Zinssatz um einen Prozentpunkt erhöht.

Im täglichen Handel hat das Rho als Risikokennziffer einer Option eher eine untergeordnete Rolle, weil die Zinsen sich in der Regel zum einen nur langsam verändern und zum anderen, weil der Einfluss auf den Optionspreis auch eher vernachlässigbar ist. 

Gehen wir einmal von einem Rho von 0,5 aus, was meiner Meinung nach schon verhältnismäßig hoch ist. Eine Zinssteigerung von 1% (im momentanen Marktumfeld sollte so eine Änderung sich mindestens über ein Jahr hinziehen), würde die Option entsprechend nur um 0,5 im Wert steigen. Wie gesagt: Über ein Jahr würde sich das ganze ziehen!

Zum Vergleich dazu: Optionen mit einer hohen Volatilität (und einem Preis des Underlyings im 20 bis 70 USD Bereich) haben am Geld häufig ein Theta von 2 oder 3. Das heißt die Option verliert 2 oder 3 USD pro Tag! Was machen da schon 0,5 USD über ein Jahr aus?

Nichtsdestotrotz sollten erfolgreiche Optionshändler auch das Rho gut verstehen, um im Extremfall vorbereitet zu sein. In diesem Zusammenhang sollte vielleicht noch einmal der risikofreie Zinssatz aus der Definition erklärt werden. 

Das Problem am risikofreien Zinssatz ist nämlich, dass es diesen nur in theoretischen Modellen gibt. Fragt euch einfach selbst, wo man denn bitte ohne jedes Risiko für etwas Zinsen bekommt. Die einen denken jetzt vielleicht an ein Tagesgeldkonto, aber auch hier besteht das Risiko, dass die Bank dahinter pleite geht.

Da es also am Markt keinen risikofreien Zins gibt, greift man auf fast risikofreie Zinsen zurück. Das könnte zum Beispiel der Einlagenzinssatz der Zentralbanken sein oder auch der implizite Zins 10-jähriger Staatsanleihen von AAA bewerteten Ländern. 

Institutionelle Investoren nehmen allerdings nichts davon, sondern benutzen stattdessen die 3-Monats-EUR-Swapkurve oder die 3-Monats-USD-Swapkurve. Diese Swapkurven jetzt zu erklären würde allerdings den Rahmen dieses Artikels sprengen. 

Da sowohl Swapkurven, Einlagenzinssätze oder Zinsen von Staatsanleihen sehr stark miteinander korrelieren, spielt es für euch keine Rolle welchen Zins ihr euch anschaut. Ein Anstieg der Swapkurve um ein Prozent führt sehr wahrscheinlich auch zu einem Anstieg der Einlagenzinssätze um ein Prozent (oder anderes herum).

Lasst uns aber nicht den Fokus auf das Rho verlieren. Hierzu sei noch zu erwähnen, dass immer gilt:

• Calls haben immer ein positives Rho. D.h. steigt der Zins, dann steigt dadurch auch der Optionspreis.
• Puts haben immer ein negatives positives Rho. D.h. steigt der Zins, dann sinkt dadurch auch der Optionspreis.

Zusätzlich wird das Rho aber auch noch durch die Restlaufzeit beeinflusst und ob eine Option sich im Geld, aus dem Geld oder am Geld befindet. Das Rho einer Option wird nämlich mit zunehmender Restlaufzeit der Option immer größer. 

Das Rho ist für Optionen außerdem am niedrigsten, wenn sich die Option außerhalb des Geldes befindet. Es ist dafür am höchsten, wenn sich die Option leicht im Geld befindet und nimmt dann wieder leicht ab, je mehr man sich in das Geld hinein bewegt.

Omega

Das Omega einer Option gibt an, um wie viel Prozent sich der Preis einer Option ändert, wenn der Wert des Underlyings um ein Prozent steigt oder fällt. D.h. bei einem Omega von 5 würde der Wert der Option um 5% steigen, wenn sich der Wert des Underlyings um 1% erhöht.

Diese Definition klingt doch sehr ähnlich wie die Definition des Deltas allerdings gibt es einen kleinen, aber feinen Unterschied. Während das Delta die Preisänderung der Option in absoluten Werten beschreibt, so beschreibt das Omega die Preisänderung der Option in relativen Werten.

Nehmen wir einfach an es gibt eine Option mit einem Delta von 0,5 und eine Option mit einem Omega von 0,5. In beiden Fällen ist der Preis des Underlyings 75 EUR und die Optionen kosten in beiden Fällen 25 EUR. 

Steigt das Underlying nun um 0,75 EUR (d.h. ein Prozent), dann steigt die Option mit einem Delta von 0,5 um 0,375 EUR (Delta mal absoluter Preisänderung von 75 Cent) aber die Option mit einem Omega von 0,5 steigt um 0,5% bzw. 0,125 EUR. (Omega mal relativer Preisänderung von einem Prozent mal aktuellem Wert der Option).

Es ist natürlich jedem selber überlassen, ob er im aktiven Optionshandel lieber mit relativen Preisänderungen oder mit absoluten Preisänderungen rechnet, aber bei den meisten Händlern hat sich dennoch das Delta als wichtigste Risikokennziffer herausgebildet und nicht das Omega.

Ich persönliche nutze das Omega lieber als Angabe über den Hebel einer Option. Wenn das Omega einer Option zum Beispiel 2 beträgt, dann weiß ich, dass jede Preisänderung des Underlyings den Preis meiner Option genau um das doppelte verändert. 

Ein Investment über 1.000 EUR in eine Aktie, die um 10% nach oben steigt, würde mir 100 EUR Gewinn einbringen aber ein Investment über 1.000 EUR in die genannte Option mit Omega von 2 würde mir bei einem Preisanstieg der Aktie von 10% einen Gewinn von 200 EUR einbringen.

Weniger bekannte Greeks

Die oben genannten Griechen sind die wichtigsten Risikokennzahlen einer Option und jeder Händler sollte damit etwas anfangen können. Allerdings gibt es noch zahlreiche andere Griechen, die im normalen Handel allerdings nur wenig Beachtung finden. 

Mathematisch betrachtet handelt es sich um die zweiten oder dritten Ableitungen der oben schon genannten Parameter und lange Zeit hat sich niemand dafür interessiert, weil es einfach zu schwer war diese Werte zu berechnen aber dank moderner Computer ist das nun auch relativ einfach, weswegen zumindest professionelle Trader auch immer häufiger auf diese Werte schauen.

Nur damit ihr einmal davon gehört habt, habe ich euch unten noch ein paar weitere Greeks und deren Bedeutung aufgelistet. Allerdings solltet ihr bei diesen Greeks immer beachten, dass deren Definition manchmal unterschiedlich sein kann, je nachdem was für ein Buch man gerade zu dem Thema liest. 

Das liegt einfach daran, dass diese Griechen in unterschiedlichen Preismodellen unterschiedlich bezeichnet werden und es deswegen keine eindeutige Definition dafür gibt. So wird das Omega auch häufig als Lambda bezeichnet. 

Am geläufigsten sind allerdings die folgenden Definitionen:

• Das Epsilon einer Option gibt an, um wie viel Prozent sich der Preis der Option ändert, wenn die Dividendenrendite des Underlyings um ein Prozent steigt oder fällt. D.h. bei einem Epsilon von 0,1 würde der Wert der Option um 0,1 Prozent zunehmen, wenn die Dividendenrendite des Underlyings um ein Prozent steigt.

• Das Vomma einer Option gibt an, um wie viel sich das Vega der Option ändert, wenn sich die implizite Volatilität um einen Prozentpunk ändert. 

• Das Vera einer Option gibt an, um wie viel sich das Rho der Option ändert, wenn sich die implizite Volatilität um einen Prozentpunk ändert. 

• Das Speed einer Option gibt an, um wieviel sich das Gamma der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt. D.h. bei einem Gamma von 0,3 und einem Speed von 0,1 würde das Gamma der Option um 0,1 auf 0,4 steigen, wenn sich der Wert des Underlyings um einen Euro erhöht.

• Das Zomma einer Option gibt an, um wie viel sich das Gamma der Option ändert, wenn sich die implizite Volatilität um einen Prozentpunk ändert. 

• Das Color einer Option gibt an, um wieviel sich das Gamma der Option mit kürzer werdender Restlaufzeit verändert. 

• Das Ultima einer Option gibt an, um wie viel sich das Vomma der Option ändert, wenn sich die implizite Volatilität um einen Prozentpunk ändert.