Das Theta einer Option ist gerade für Optionsverkäufer einer der wichtigsten Griechen aber leider auch einer der am wenigsten verstanden Greeks. Grund genug uns dem Theta etwas genauer zuzuwenden, damit ihr beim Verkauf eurer Optionen genau versteht, wo und wann ihr einen Gewinn machen könnt. 

Es gibt also viel über das Theta zu verstehen und im weiteren Erkläre ich euch alle Details und gebe euch ein paar zusätzliche Tipps, wie ihr das Theta in euren täglichen Optionshandel einfließen lassen könnt.

Was ist das Theta einer Option

Das Theta einer Option gibt an, um wieviel sich der Preis einer Option jeden Tag verringert und wenn ihr neu im Optionshandel seid, dann fragt ihr euch jetzt sicherlich, warum eine Option denn überhaupt im Laufe der Zeit weniger wert sein soll.

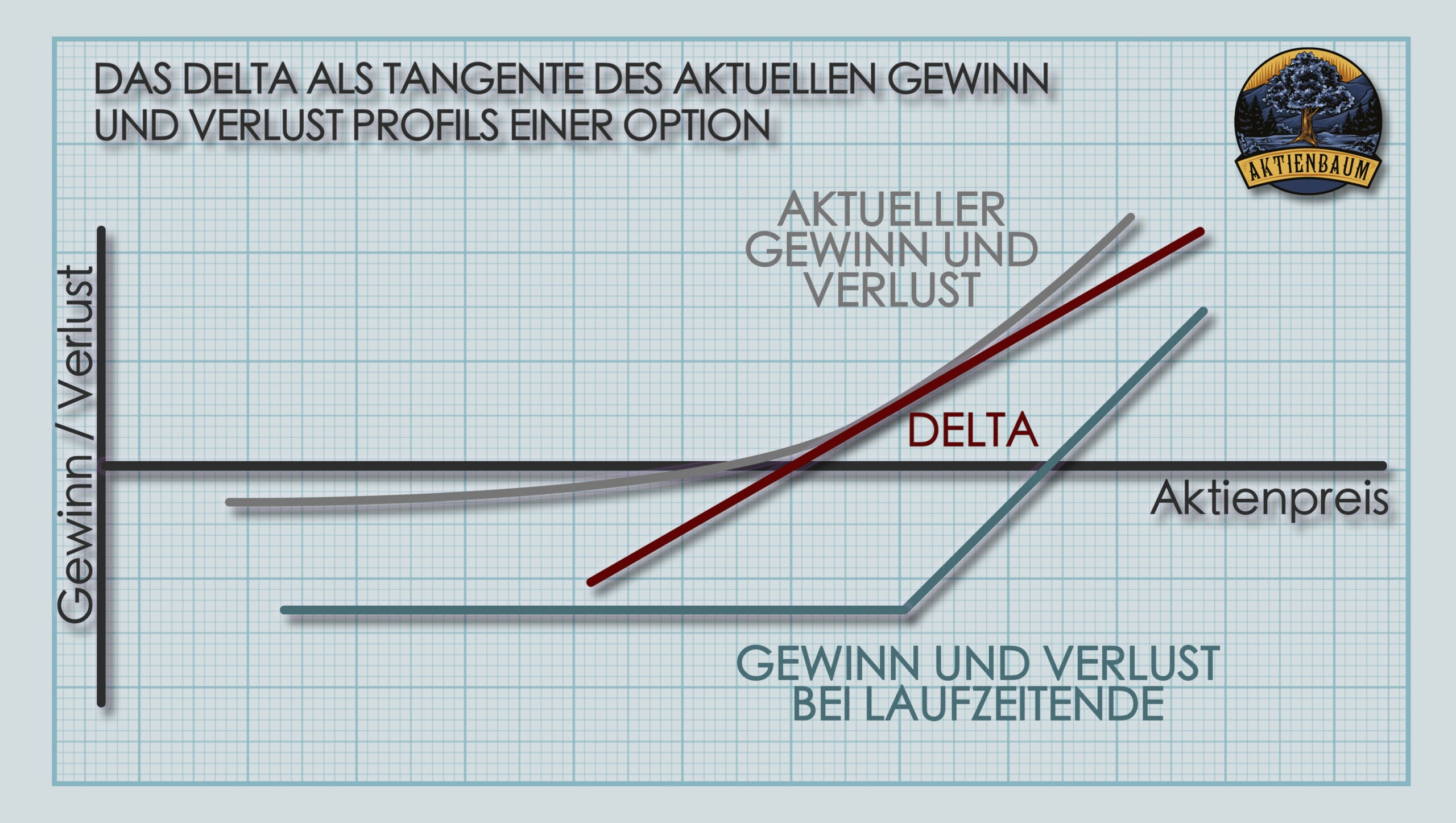
Um also den Zusammenhang zwischen dem Theta einer Option und dem Wert der Option besser verstehen zu können, müssen wir noch einmal ganz kurz darüber sprechen, wie sich der Wert einer Option überhaupt zusammensetzt.

Optionen besitzen einen inneren Wert und einen Zeitwert. Der innere Wert, ist der Wert, den die Option bei aktuellem Preis des Underlyings zum Laufzeitende auszahlen würde und der Zeitwert ist der Wert, den die Option zusätzlich noch besitzt, weil es eine Wahrscheinlichkeit gibt, dass der innere Wert noch steigen könnte.

Am besten versteht man den Zeitwert einer Option sicherlich, wenn man das Auszahlungsprofil einer Option bei Laufzeitende mit dem Auszahlungsprofil der selben Option mit noch Restlaufzeit vergleicht.

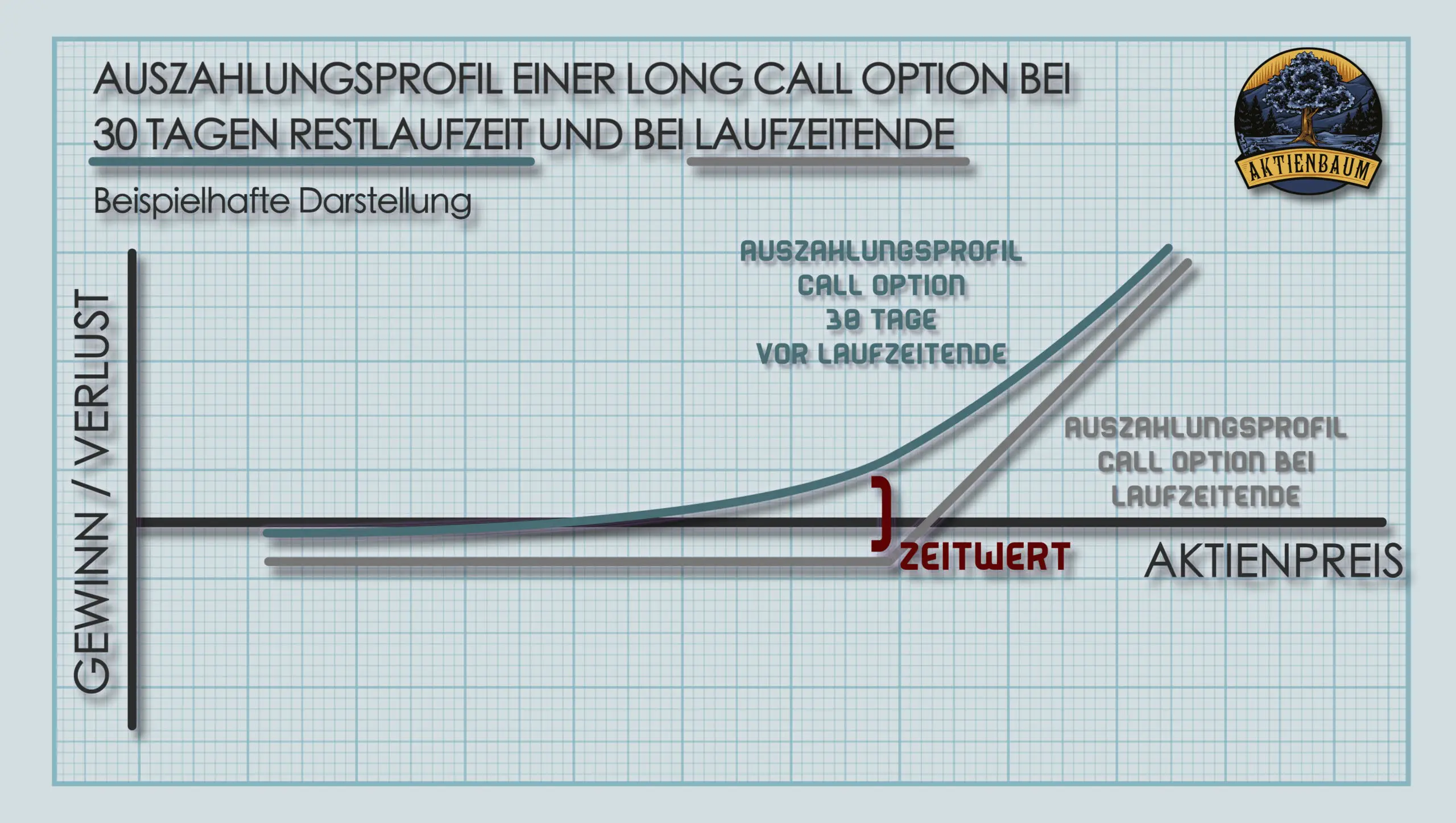
In der Grafik kann man gut sehen, wie das Auszahlungsprofil der Option bei Laufzeitende ist (graue Linie). Der aktuelle Wert liegt aber immer mal mehr oder mal weniger darüber und dieser zusätzliche Wert ist der Zeitwert der Option. Der Zeitwert repräsentiert dabei die Wahrscheinlichkeit, dass der innere Wert noch steigen bzw. fallen kann, weil sich die Option ja schließlich noch im Laufe der Restlaufzeit ins Geld bewegen kann.

Umso kürzer die Restlaufzeit ist, desto unwahrscheinlicher ist es aber, dass die Option sich noch ins Geld bewegt und entsprechend nimmt der Zeitwert einer Option mit kürzer werdender Restlaufzeit ab. Genau diesen Wertverlust gibt nun das Theta einer Option an.

Das Theta ist dabei immer negativ, da es aus Sicht des Käufers einer Option angegeben wird. D.h. wenn ihr eine Apple Option kauft und deren Theta momentan -3 beträgt, dann wird der Wert der Option morgen 3 USD weniger betragen (zumindest sofern alle anderen Faktoren, also Preis des Underlyings, Zins, Volatilität usw., gleich bleiben).

Für den Verkäufer einer Option ist das Theta aber ein Gewinn, da dessen Option, die er verkauft hat, täglich an Wert verliert und er sie somit günstiger zurückkaufen kann.

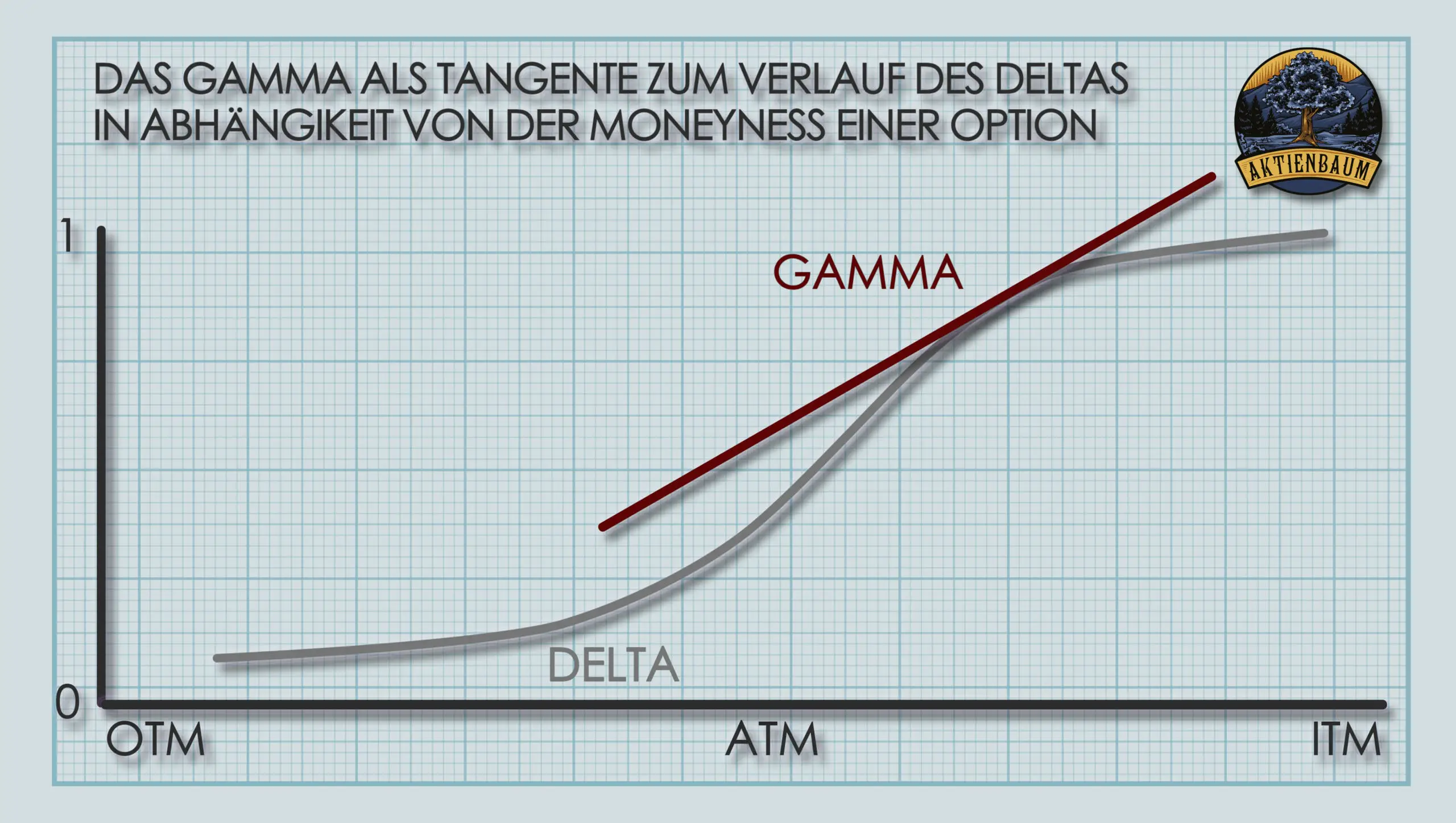
Das Theta ist allerdings kein konstanter Wert und hängt von vielen Markteinflüssen wie der Restlaufzeit, der Volatilität oder dem risikolosen Zins ab. Den aber wahrscheinlich größten Einfluss auf das Theta hat die sogenannte Moneyness der Option. Also wie sehr sich die Option schon im Geld befindet. Eine genaue Erklärung wie das Theta durch die verschiedenen Faktoren beeinflusst wird, erkläre ich euch weiter unten.

Die Berechnung des Thetas einer Option

Anders als zum Beispiel beim Delta oder dem Gamma einer Option kann man das Theta nur mithilfe eines mathematischen Optionspreismodels berechnen. Ich erkläre euch gleich, wie ihr das machen könnt, allerdings will ich an dieser Stelle auch hinweisen, dass es in aller Regel gar nicht notwendig ist, dass ihr das Theta einer Option selbst berechnet, weil ihr diese Information auch online auf verschiedenen Webseiten einsehen könnt oder einfach mithilfe meines Optionspreisrechners selbst berechnen könnt bzw. ein guter Broker euch die Information auch immer bereitstellt.

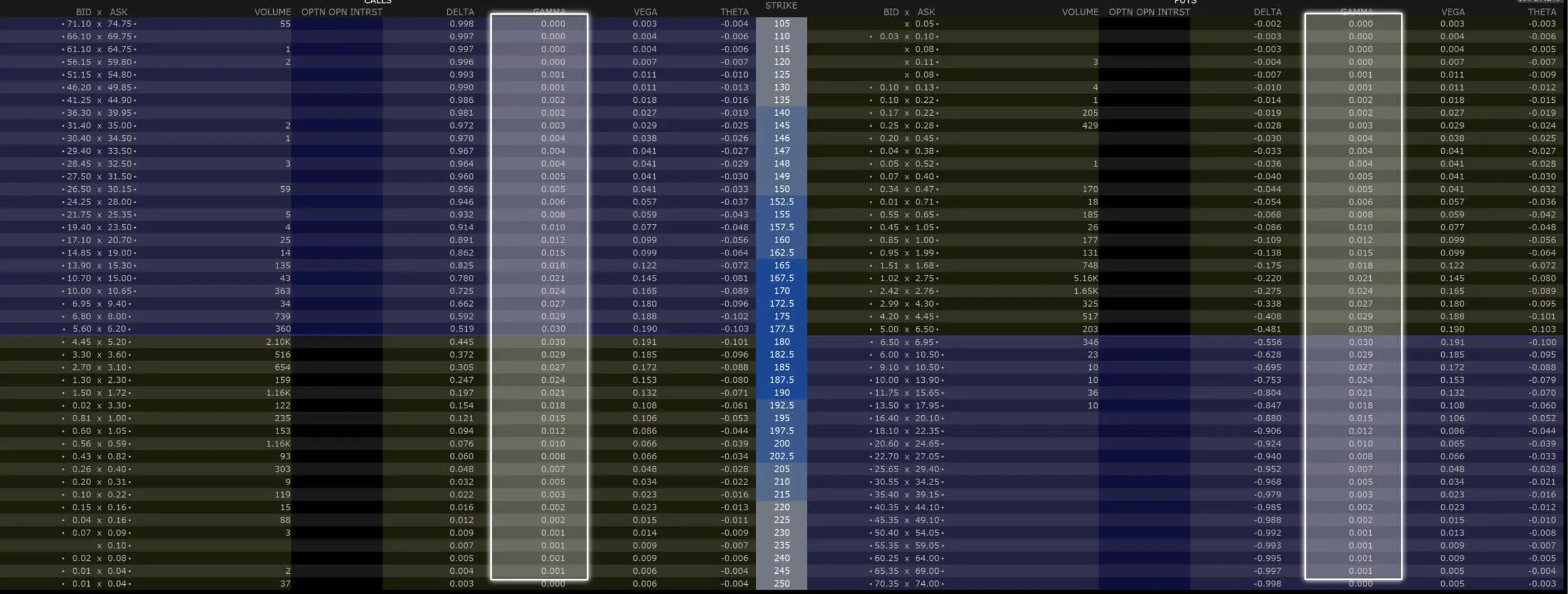
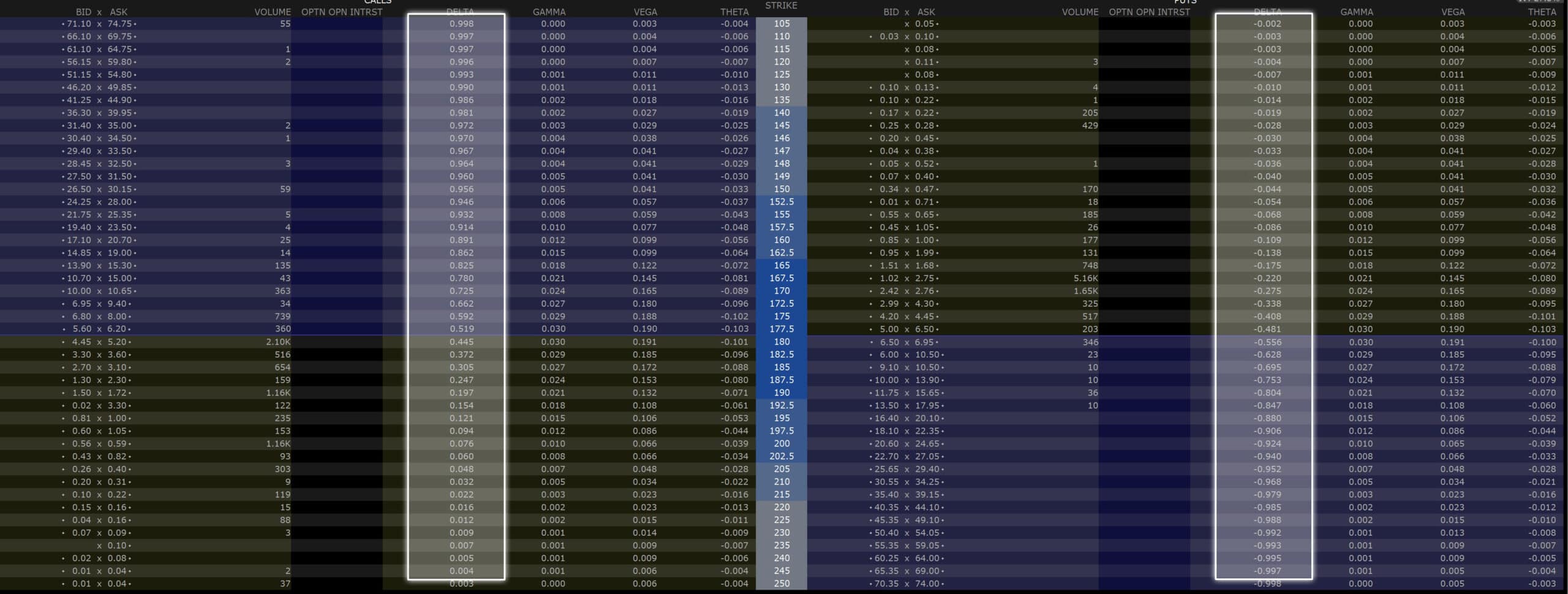
Ich nutze für den Optionshandel zum Beispiel den Broker Estably (bis vor kurzem noch unter „Banx Broker“ bekannt) und dort wird das Theta als Standardinformation bei jeder Option direkt mit angezeigt. D.h. noch bevor ich überhaupt eine Option kaufe oder verkaufe, erhalte ich alle Informationen direkt von meinem Broker, die ich benötige.

Das Theta wird bei eurem Broker dabei in der sogenannten Option Chain angezeigt. Dort findet ihr alle Call und Put Optionen geordnet nach dem jeweiligen Strike Preis für eine bestimmte Laufzeit. Neben dem Preis für jede Option werden in der Option Chain aber auch alle Greeks inklusive dem Theta angezeigt. Hier mal ein Screenshot, wie das ganze bei Estably aussieht.

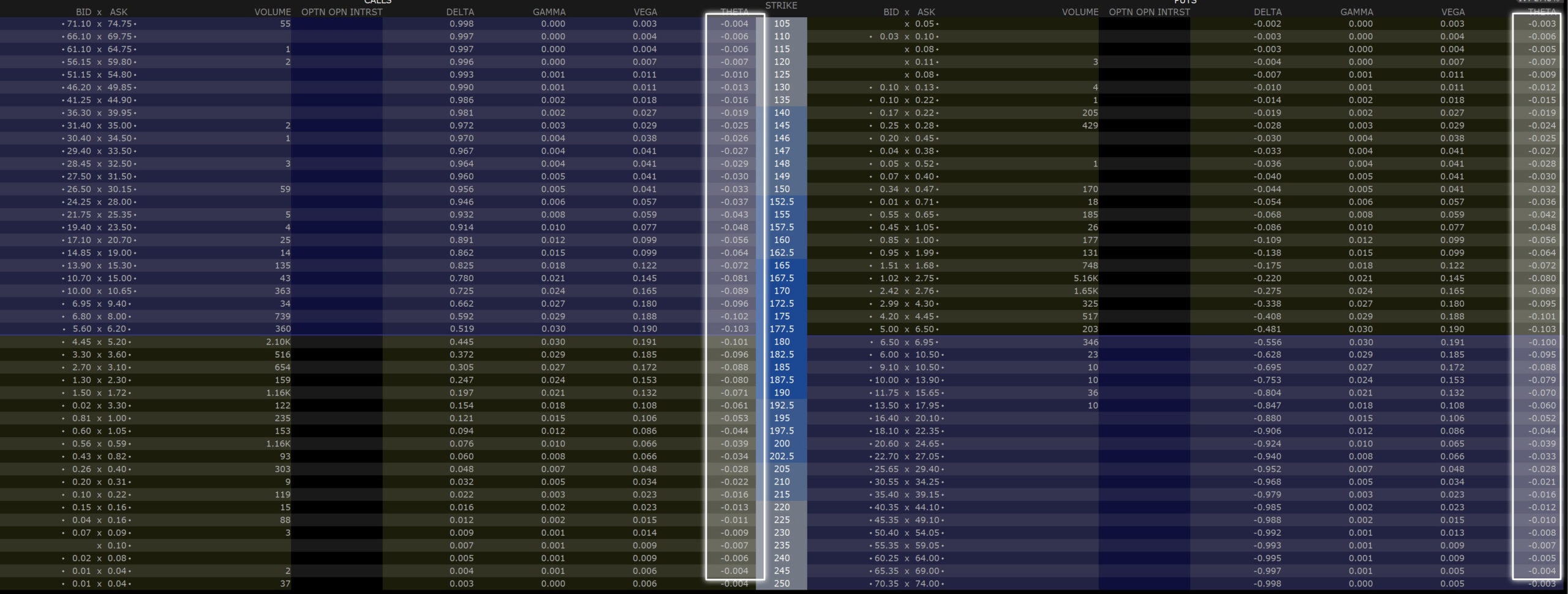
Wenn ihr auch Optionen handeln möchtet, dann kann ich euch Estably wirklich nur empfehlen. Im Hintergrund nutzt Estably Interactive Brokers, was ein Tool ist, das auch von Profis genutzt wird. Entsprechend bekommt ihr dort alle Informationen, die für den Optionshandel notwendig sind und könnt euch auch alles so individuell einrichten, wie ihr möchtet.

Wenn ihr ein Depot bei Estably eröffnen wollt, dann könnt ihr das über diesen Link machen*. Das gibt euch Zugriff auf ein wirklich tolles Trading Tool, einen günstigen Broker und ihr unterstützt gleichzeitig noch meine Arbeit, weil ich bei einer Depoteröffnung eine kleine Gebühr von Estably bekomme (ohne, dass das ganze für euch teurer wird).

Aber zurück zum Thema. Auch wenn ihr das Theta einer Option selbst nicht berechnen müsst, ist es dennoch ganz gut zu wissen, wie es berechnet wird, damit ihr besser verstehen könnt wie sich das Theta einer Option verändert je nachdem welche Marktveränderungen eintreten.

Mithilfe eines Optionspreismodells

Grundsätzlich gibt es verschiedene mathematische Modelle zur Preisberechnung von Optionen, allerdings hat sich in der Praxis das sogenannte „Black-Scholes-Modell“ durchgesetzt, dass nach den beiden US-Amerikaner Fischer Black und Myron Scholes benannt wurde, die dieses Modell 1973 veröffentlichten.

Das besondere am Black-Scholes Modell ist, dass es ermöglichte, die Preisberechnung einer Option auf eine mehr oder weniger einfache mathematische Formel herunterzubrechen, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.

Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt.

Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.

Das Theta ist dabei die erste Ableitung des Black-Scholes Modells nach der Restlaufzeit weswegen das Theta auch angibt, um wie viel sich der Preis der Option ändert, wenn sich die Restlaufzeit um einen Tag verringert.

Die Formel bzw. besser gesagt Formeln für das Black-Scholes Modell sind relativ komplex und ich möchte hier auch nicht zu sehr ins Detail gehen, weswegen ich einfach auf Wikipedia verweisen würde, wenn ihr gern mehr dazu erfahren wollt.

Der Zusammenhang des Thetas mit anderen Markteinflüssen

Moneyness

Wie ich weiter oben schon beschrieben habe, hat von allen Faktoren, die das Theta beeinflussen, der Preis des Underlyings bzw. die sogenannte „Moneyness“ den größten Einfluss auf das Theta.

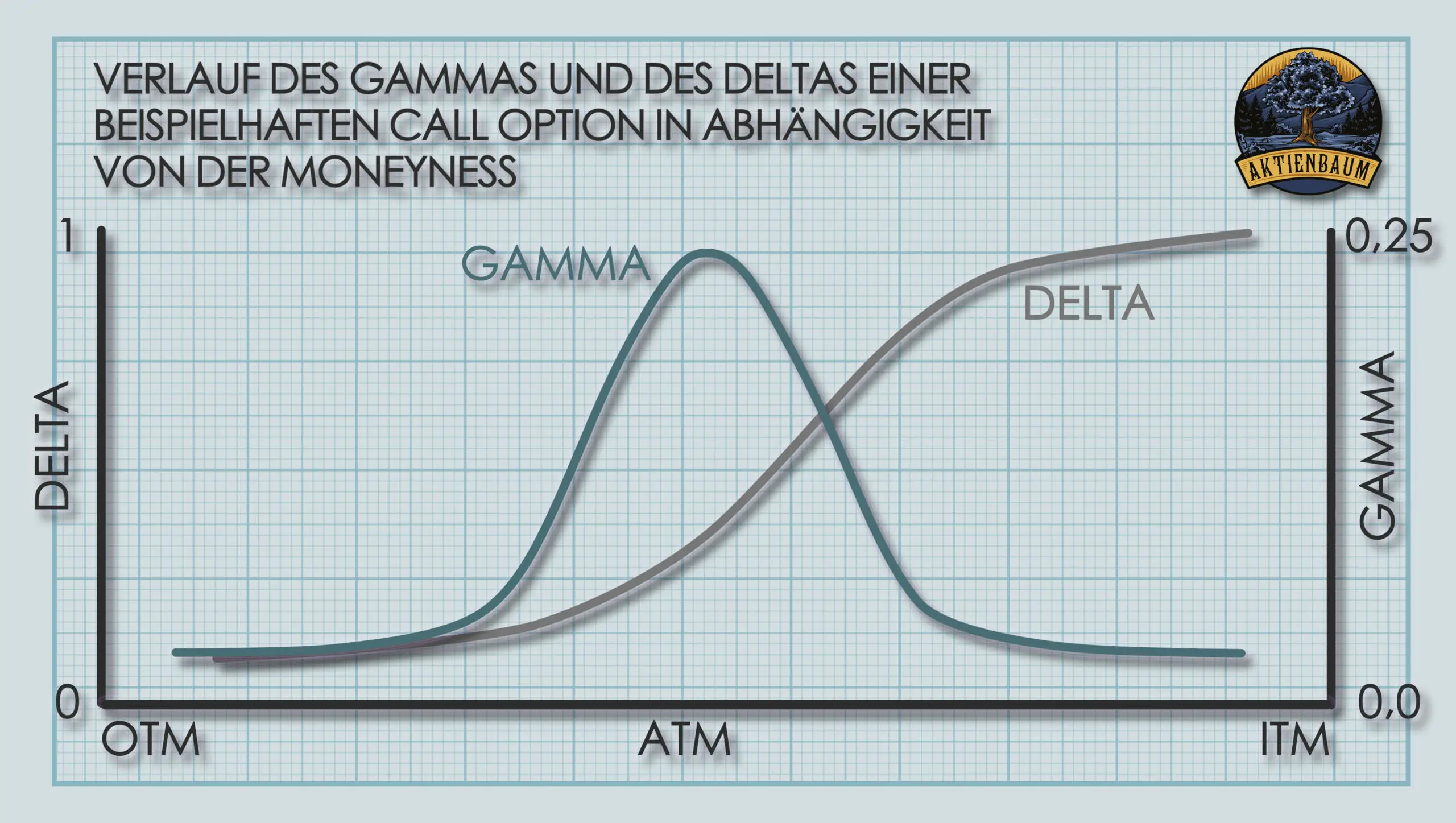
Das Theta einer Option ist dabei umso höher, je größer der Zeitwert der Option ist und der Zeitwert ist immer dann am höchsten, wenn sich die Option am Geld befindet (unter der Annahme, dass alle anderen Einflussfaktoren konstant bleiben), also wenn der Kurs des Underlyings sehr nah am Strike der Option ist.

Das macht auch Sinn, da Optionen am Geld noch eine sehr hohe Wahrscheinlichkeit haben ins Geld, also in den Gewinnbereich, zu gelangen. Der Zeitwert drückt genau diese Wahrscheinlichkeit aus und entsprechend ist er am Geld am höchsten.

Der Zeitwert bzw. das Theta ist allerdings nicht dann am höchsten, wenn der Kurs des Underlyings genau dem Strikepreis entspricht, sondern in der Regel, wenn der Kurs des Underlyings leicht über dem Strikepreis liegt. Mathematisch kann man diesen Punkt des maximalen Zeitwertes sogar exakt berechnen, aber das würde jetzt den Rahmen dieses Artikels sprengen.

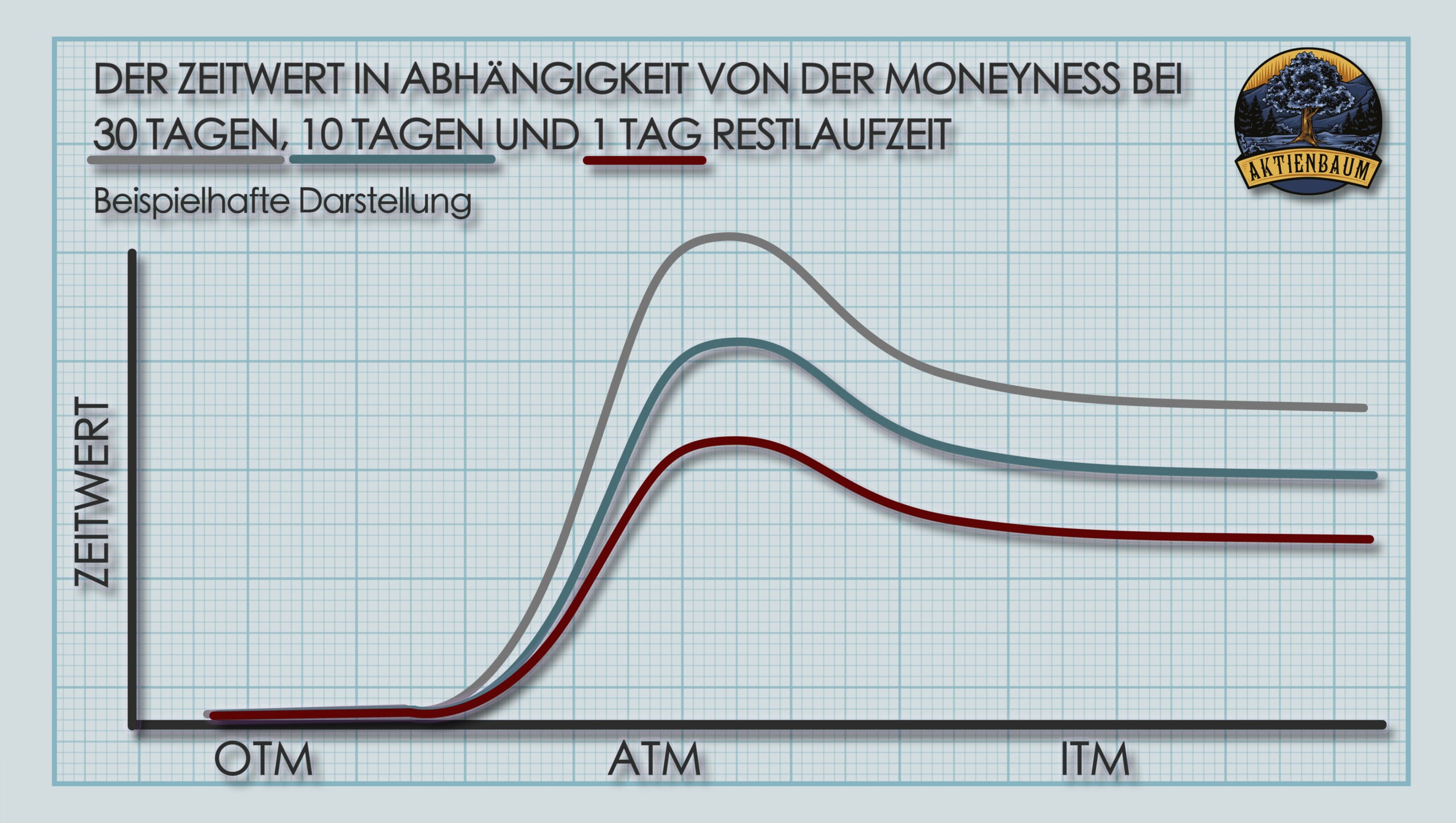
Für Optionen, die sich bereits im oder außerhalb des Geldes befinden, ist die Auszahlungshöhe bei Restlaufzeit bereits mehr oder weniger sicher. Entweder ist sie Null (bei OTM Optionen) oder sie ist der innere Wert (bei ITM Optionen). Entsprechend haben OTM und ITM Optionen nur einen sehr geringen Zeitwert, allerdings muss man auch sagen, dass der Zeitwert für OTM und ATM Optionen nicht identisch ist.

Optionen, die sich extrem weit außerhalb des Geldes befinden, haben nämlich in aller Regel gar keinen Zeitwert mehr bzw. ein Theta von null ganz egal wie lang die Restlaufzeit ist.

Im Gegensatz dazu haben Optionen, die sich extrem tief im Geld befinden immer noch einen restlichen Zeitwert und somit auch noch ein positives Theta. Allerdings bleibt der Zeitwert einer Option im ITM Bereich in der Regel konstant, ganz egal wie tief sich die Option im Geld befindet.

Restlaufzeit

Wie hoch das Theta einer Option ausfällt, hängt allerdings nicht nur von deren Moneyness ab, sondern sehr stark auch von deren Restlaufzeit.

Der Zeitwert einer Option nimmt nämlich nicht gleichmäßig ab, sondern verringert sich für die meisten Optionen bei langer Restlaufzeit nur wenig aber dafür sehr stark wenige Tage vor Laufzeitende. Im Umkehrschluss heißt das also, dass das Theta einer Option bei sehr langer Restlaufzeit nur niedrig ist und erst kurz vor Laufzeitende schnell ansteigt.

Dabei ist wichtig zu wissen, dass das Theta von ITM, OTM und ATM bei kürzer werdender Restlaufzeit nicht gleichmäßig zunimmt.

Das Theta von Optionen, die sich außerhalb des Geldes befinden, ist nämlich bei langer Restlaufzeit höher als bei kürzerer Restlaufzeit. D.h. OTM Optionen verlieren bereits einen größeren Teil ihres Zeitwerts in der ersten Hälfte ihres Lebens, während das Theta dann in der zweiten Hälfte eher abnimmt.

Im Gegensatz dazu ist das Theta von Optionen, die sich im Geld befinden, relativ konstant über die komplette Restlaufzeit. Das heißt der Zeitwert von ITM Optionen nimmt täglich um fast den selben Wert ab.

Die Veränderung des Thetas von Optionen, die sich am Geld befinden, entspricht wiederum dem klassischen Verständnis zum Verlauf des Thetas über die Laufzeit der Option. D.h. das Theta ist bei noch langen Restlaufzeiten sehr klein und steigt dann immer mehr an, je näher die Option an das Laufzeitende kommt.

Je nach Handelsstrategie die ihr verfolgt, solltet ihr also Optionen mit ganz bestimmten Eigenschaften kaufen oder verkaufen. In welchen Marktlagen welche Optionsstrategie die beste ist bzw. welche Optionen ihr auswählen solltet, verrate ich euch in diesem Artikel. Die wichtigsten Theta Strategien erkläre ich euch in der folgenden Box.

Volatilität

Über die Volatilität und ihren Einfluss auf das Theta einer Option habe ich nun schon an verschiedenen Stellen in diesem Artikel gesprochen, aber ich möchte euch dennoch noch ein paar Details dazu mitgeben.

Wie immer gilt auch bei der Volatilität die Logik, dass das Theta dann besonders hoch ist, wenn der Zeitwert besonders hoch ist (unter der Annahme, dass alle anderen Faktoren gleich geblieben sind).

Der Einfluss der Volatilität auf den Zeitwert ist dabei ganz einfach. Umso höher die implizite Volatilität ist, desto höher ist auch der Zeitwert. Die Erklärung dafür ist, dass bei hoher Volatilität die Wahrscheinlichkeit der Option sich ins Geld zu bewegen, höher ist als bei niedriger Volatilität.

Eine Aktie mit aktuellem Wert von 100 EUR hat einfach eine höhere Chance in zwei Wochen auf 120 EUR anzusteigen, wenn sie täglich um 10 EUR schwankt als dieselbe Aktie die täglich um 1 EUR schwankt.

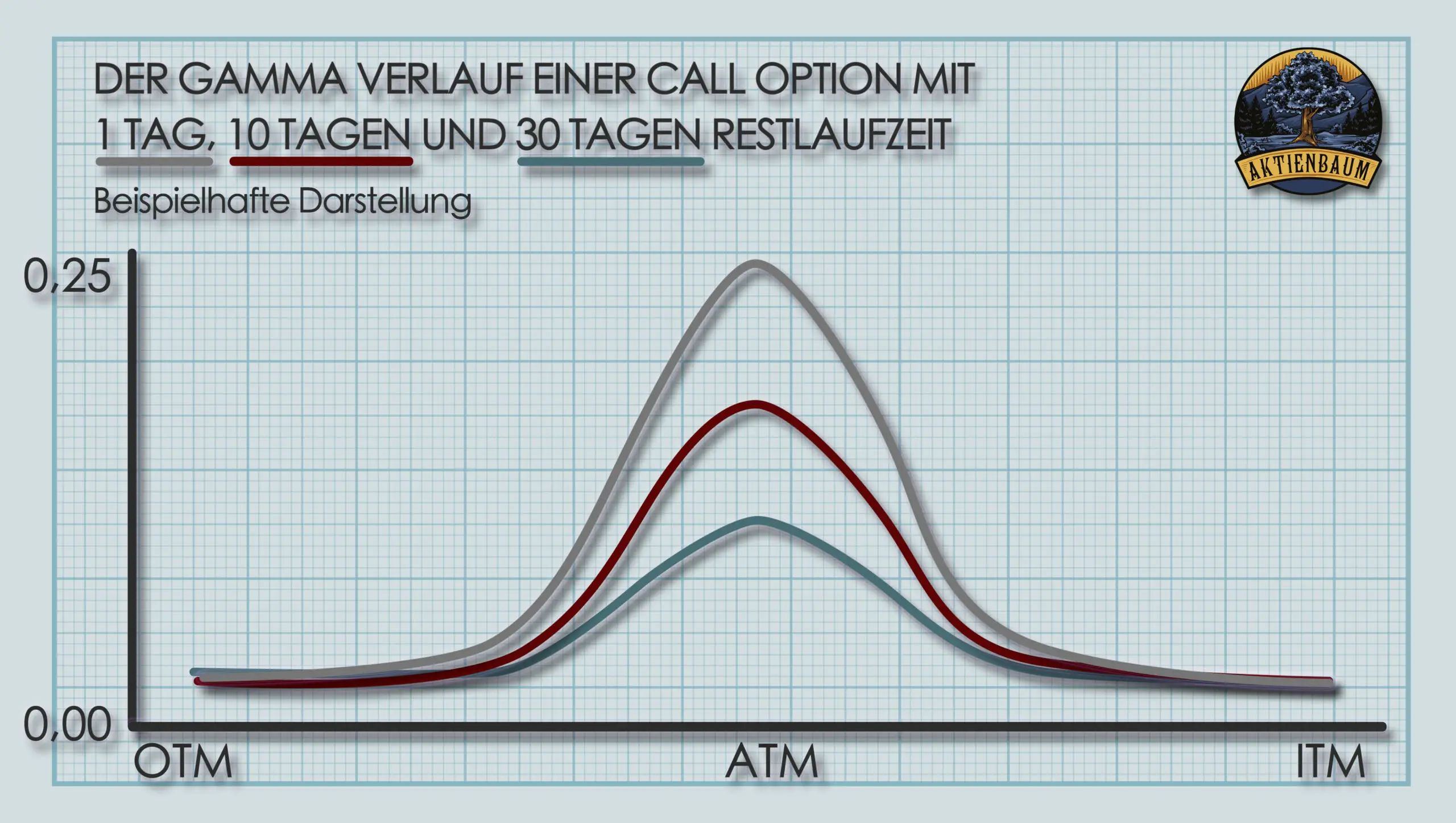
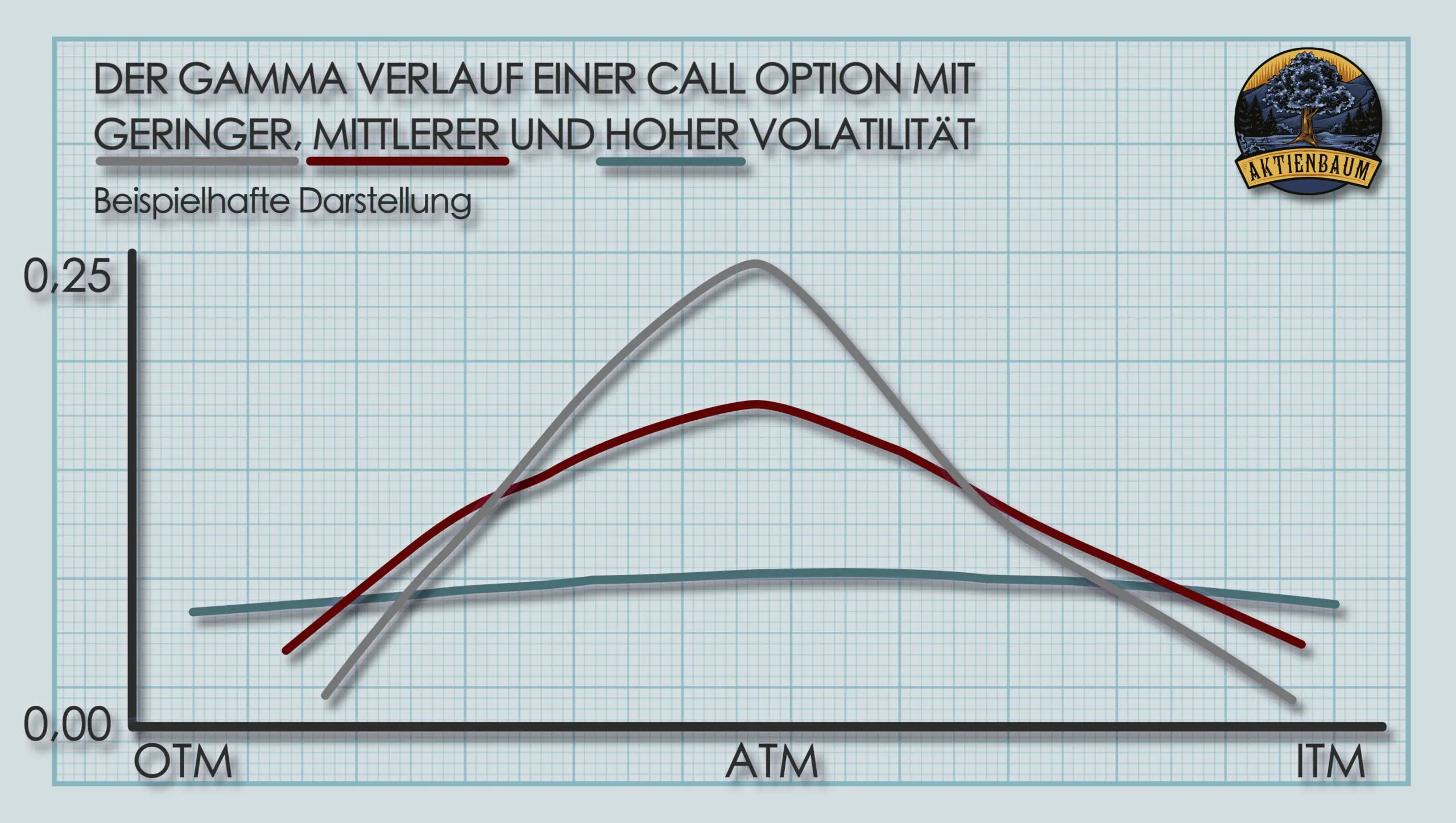
Interessant wird es aber, wenn man sich den Zeitwert einer Option im Zeitverlauf bis Laufzeitende bei unterschiedlichen Volatilitäten anschaut, wie ich euch in der unten stehenden Grafik zeige.

In der Grafik seht ihr dabei, wie sich der Zeitwert einer ATM Option bis Laufzeitende verändert in Abhängigkeit von der impliziten Volatilität. Ist die Volatilität des Underlyings relativ niedrig (kleiner 35%), dann verläuft der Zeitwert nahezu identisch. D.h. in diesem Fall hat die Volatilität keinen großen Einfluss auf das Theta einer Option.

Umso höher die Volatilität aber wird, desto schneller verliert aber auch der Zeitwert an Wert bei kürzer werdender Restlaufzeit was bedeutet, dass das Theta in diesen Fällen deutlich höher ist. Am besten seht ihr das in der Grafik für den Zeitraum kurz vor Laufzeitende. In dem Fall verläuft der Zeitwertverfall deutlich rapider bei höherer Volatilität, was mit einem deutlich höherem Theta der Option einhergeht.

Risikofreie Zins

Die meisten Optionshändler beachten den risikofreien Zins in aller Regel gar nicht, weil dessen Einfluss einfach zu gering auf den Wert einer Option ist (was auch stimmt) aber der Vollständigkeit halber möchte ich dessen Zusammenhang zum Theta trotzdem kurz erklären.

Der risikofreie Zins ist der Zins, zudem man sich am Markt risikofrei Geld leihen kann. Die meisten Privatanleger verstehen darunter so etwas wie den aktuellen Tagesgeldzinssatz aber für professionelle Investoren wird damit eigentlich der Interbanken-Zinssatz gemeint. Also der Zins, zu dem sich Banken untereinander Geld leihen.

Der Einfluss des risikofreien Zins auf das Theta ist dabei, dass umso höher der risikofreie Zins ist, desto höher ist auch der Zeitwert einer Option, was auch mit einem höheren Theta (bei sonst gleichbleibenden Einflussfaktoren) einhergeht.

Das heißt, ist der risikofreie Zins besonders hoch, dann hat eine Option auch ein höheres Theta als die selbe Option bei geringerem risikofreien Zins.

Der Grund, warum die meisten Optionshändler den risikofreien Zins aber in aller Regel nicht beachten ist, dass der Einfluss des Zins auf den Kurs bzw. den Zeitwert einer Option nur sehr gering ist und wenn überhaupt nur bei extrem hohen Zinssätzen relevant wird. Zusätzlich handeln die meisten Privatanleger Optionen auch nur über sehr kurze Zeitperioden und in so kurzen Perioden verändert sich der risikofreie Zins in aller Regel auch nur sehr wenig.

Wenn es um den Handel mit Optionen geht, heißt immer wieder, dass statistisch betrachtet das Verkaufen von Optionen mehr Sinn machen würde, weil angeblich circa 80% aller Optionen wertlos verfallen, aber stimmt das eigentlich? Ich habe es einfach selbst nachgerechnet und dafür 555.746 Optionen für euch analysiert, um euch zu zeigen, wie viele Optionen eigentlich wirklich wertlos verfallen.

Wenn also nur 62% der Optionen wirklich wertlos zum Laufzeitende verfallen, warum hält sich dann der Mythos so hartnäckig, dass angeblich 80% (in manchen Quellen sogar bis zu 90%) aller Optionen wertlos verfallen? 

Das hat mit einem allgemeinen Missverständnis über den Verfall von Optionen zu tun. Nach Aussagen diverser Webseiten hätte die Chicagoer Börse (CBOE) einmal veröffentlicht, dass lediglich 10% bis 20% aller Optionen bei Laufzeitende ausgeübt werden (ich konnte diese Aussage der CBOE allerdings selbst nirgends finden).

Daraus wurde nun geschlussfolgert, dass wenn lediglich 20% der Optionen ausgeübt werden, es doch 80% der Optionen sein müssen, die nicht ausgeübt werden. Klingt eigentlich logisch aber diese Schlussfolgerung ist komplett falsch.

Der Grund dafür ist einfach, dass circa 60% aller Optionen nie bis Laufzeitende gehalten werden, sondern vorher glattgestellt werden (warum ihr das auch machen solltet, erkläre ich in diesem Artikel). Das heißt circa 60% aller Optionen laufen niemals bis Laufzeitende, um dann eventuell ausgeübt zu werden oder nicht.  Entsprechend können wir aus der Menge an ausgeübten Optionen nicht schlussfolgern wie viele Optionen nicht ausgeübt werden.

Wenn wir also wissen wollen, wie viele Optionen nicht ausgeübt werden, bleibt einem nichts anderes übrig als einfach selbst nachzuzählen und genau das habe ich gemacht. Mit insgesamt 555.746 Optionen, um endlich herauszufinden wie viele Optionen wirklich wertlos verfallen.

Ich habe mir deshalb alle Optionen mehrerer Aktien und Indizes für unterschiedliche Laufzeiten angeschaut, die am 04.01.2021 gekauft oder verkauft wurden und habe dann geprüft, wie viele dieser Optionen bei Laufzeitende im Geld waren.

Ich habe dabei Aktien aus unterschiedlichen Bereichen gewählt, Optionen mit unterschiedlicher Laufzeit und mir sowohl Put als auch Calls angeschaut. Meine Ergebnisse könnt ihr in den folgenden Tabellen sehen. 

Von insgesamt 555.746 Optionen wurden am Laufzeitende 210.982 ausgeübt, was circa 38% entspricht bzw. 62%, die nicht ausgeübt wurden.  Wie ihr der Tabelle aber entnehmen könnt, ist das nur der Durchschnittswert über alle Optionen und die Ausübungsquote variiert doch stark. 

Mit 22% wurden am seltensten die Optionen von Amazon ausgeübt während insgesamt 45% aller Microsoft Aktien ausgeübt wurden. 

Ich habe die Aktien bzw. Indizes auch in Tech-Aktien und Nicht-Tech-Aktien eingeteilt, um zu schauen, ob es hier eventuell ebenfalls einen deutlichen Unterschied gibt, und in der Tat unterscheiden sich die beiden Sektoren doch stark voneinander.

Während 39% aller Optionen auf Tech-Aktien ausgeübt wurden, waren es doch lediglich 27% auf Nicht-Tech-Aktien. Der Unterschied ist für mich allerdings nicht so überraschend, weil Technologie-Aktien in aller Regel auch eine höhere Volatilität haben und entsprechend häufiger im Geld landen können.

Wer von euch also gern Optionen verkauft, der sollte dies eher bei Nicht-Tech-Aktien machen, um eine höhere Wahrscheinlichkeit zu haben nicht im Geld zu landen. Allerdings sind die Prämien für Optionen auf Nicht-Tech-Aktien häufig auch geringer.

Ebenfalls interessant ist der Unterschied bei Einzelaktien und Indizes.

39% aller Optionen auf Einzelaktien werden ausgeübt und lediglich 26% aller Optionen auf Indizes. Auch hier wäre die Strategie für Optionsverkäufer eher Optionen auf Indizes zu schreiben anstatt auf Einzelaktien. Für Optionskäufer wäre es genau anders herum.

Mich hat allerdings auch noch interessiert, ob es bei der Ausübungs-Quote von Optionen einen Unterschied bei deren Laufzeit gibt. Also werden eher langlaufende oder kurzlaufende Optionen ausgeübt und auch hier haben mich die Ergebnisse überrascht.

Ich habe alle Optionen und deren Laufzeiten unterteilt in weniger als 100, 200 und 300 Tagen und die Ergebnisse zeigen deutlich, dass je länger eine Option läuft, umso wahrscheinlicher ist es, dass diese auch ausgeübt wird bzw. umso unwahrscheinlicher ist es, dass sie nicht ausgeübt wird.

Zum Schluss wollte ich noch wissen, ob es auch einen Unterschied zwischen Call und Put Optionen gibt und auch hier fallen die Ergebnisse deutlich aus.

Call Optionen werden wesentlich häufiger ausgeübt als Put Optionen allerdings sollte auch erwähnt werden, dass während des Beobachtungszeitraums (2021) ein Bullenmarkt vorlag. D.h. Aktienkurse sind tendenziell gestiegen weswegen Calls häufiger im Geld landeten. 

Da langfristig betrachtet Aktienmärkte aber immer steigen, sollte das keinen großen Unterschied machen und man sollte immer mit 49% bei Call Optionen bzw. 16% bei Put Optionen rechnen.

Wenn ihr euch übrigens für meine Zahlen interessiert, so könnt ihr meine gesamte Datengrundlage und Berechnung hier als Excel Sheet und hier als Google Sheet finden.

Sollte man eine Option bis Laufzeitende halten?

Jetzt nachdem ihr wisst, wie viele Optionen wirklich ausgeübt werden, stellt ihr euch vielleicht die Frage, ob man Optionen überhaupt bis zum Ende der Laufzeit halten sollte und die einfache Antwort darauf ist: Nein.

Optionen sollten in der Regel nie bis zum Laufzeitende gehalten werden, um das Risiko einer Ausübung der Option zu umgehen und da Optionen aufgrund des zusätzlichen Zeitwerts während der Laufzeit mehr wert sind als am Ende der Laufzeit.

D.h. ein Grund Optionen nie bis zum Laufzeitende zu halten, ist das Ausübungsrisiko. Wenn ihr also nicht wollt, dass die Optionen ausgeübt werden soll (z.B. weil ihr die zugrunde liegenden Aktien kaufen oder verkaufen wollt), solltet ihr Optionen spätestens ein paar Tage vor Laufzeitende zurückkaufen.

Somit umgeht ihr, dass die Option ausgeübt wird und ihr eventuell Aktien eingebucht oder verkauft bekommt auch wenn vielleicht alles danach aussah, dass sich die Option nicht im Geld befand. 

Ich habe einfach schon zu oft gehört, dass sich eine Option am Ende der Laufzeit eigentlich nicht im Geld befand und die Option trotzdem ausgeübt wurde, weil kurz nach Ausübung eine Dividende ausgezahlt wurde oder nach Börsenschluss wichtige Unternehmensergebnisse veröffentlicht wurden.

Der zweite Grund wiederum ist nur für Käufer von Optionen relevant. Diese kaufen schließlich eine Option in der Hoffnung, dass der Preis der Option steigen wird. Entsprechend sollten Käufer die Option auch dann verkaufen, wenn ihr Preis am höchsten ist und der Wert einer Option ist (unter sonst gleichen Bedingungen) während der Laufzeit einer Option immer höher als am Ende der Laufzeit.

Der Grund hierfür ist der Zeitwert einer Option, der umso höher ist, je länger die Laufzeit der Option noch ist.

Ein entscheidender Faktor für Erfolg im Optionshandel ist das Verständnis der Griechen, und unter diesen spielt das Gamma eine wesentliche Rolle. In diesem Artikel erkläre ich, was das Gamma einer Option bedeutet und wie ihr dieses Wissen effektiv in eurem täglichen Handel mit Optionen einsetzen könnt.

Dieser Artikel behandelt das Gamma einer Option im Detail. Wenn ihr gern einen allgemeineren Überblick über alle Griechen einer Optionen haben wollt, dann könnt ihr euch auch diesen Artikel von mir durchlesen.

Was ist das Gamma

Das Gamma einer Option gibt an, um wieviel sich das Delta der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt. D.h. bei einem Delta von 0,3 und einem Gamma von 0,1 würde das Delta der Option um 0,1 auf 0,4 steigen, wenn sich der Wert des Underlyings um einen Euro erhöht.

Das Gamma einer Option kann dabei zwischen 0 und 1 liegen und da es sich um einen absoluten Wert handelt, gibt es auch keinen Unterschied bei Puts und Calls. D.h. ein Gamma von 0,1 erhöht immer das Delta einer Option um 0,1 bei einem Preisanstieg des Underlyings um eine Währungseinheit ganz egal ob Put oder Call oder Long oder Short.

Unter identischen Rahmenbedingungen, d.h. bei gleichem Strike-Preis, gleichem Underlying Kurs, gleicher Laufzeit, gleichem Zinssatz usw., ist das Gamma eines Calls und eines Puts sogar identisch.

Weil das Gamma nur zwischen 0 und 1 sein kann, kann man es aber auch als Prozentwert interpretieren in Abhängigkeit vom Kurs des Underlyings. Hat eine Option also ein Gamma von 0,05 und der Kurs des Underlyings erhöht sich um 2 EUR, dann ändert sich das Delta der Option um 5% der Aktienkursänderung. Also in diesem Fall 5% von 2, was einer Delta-Änderung von 0,1 entspricht.

Die Dezimalschreibweiße ist zwar die mathematisch korrekte Art, das Gamma zu beschreiben aber in der Praxis sagt bzw. schreibt man selten, dass eine Option ein Gamma von 0,05 oder 0,1 hat, sondern man sagt stattdessen, dass eine Option ein Gamma von 5 oder 10 hat.

Ein Gamma von 10 bedeutet somit, dass das Delta einer Call Option um 10 im Wert steigt, wenn das Underlying einen Euro im Wert ansteigt.

Berechnung des Gammas

Um das Gamma einer Option zu berechnen, gibt es grundsätzlich zwei Möglichkeiten. Die korrekte Variante ist, dass man das Gamma mithilfe eines Optionspreismodells berechnet und die weniger komplizierte Variante ist die Berechnung mithilfe von Marktdaten. Ich erkläre euch gleich beide Varianten etwas genauer, allerdings will ich an dieser Stelle auch hinweisen, dass es in aller Regel gar nicht notwendig ist, dass ihr das Gamma einer Option selbst berechnet, weil ihr diese Information auch online auf verschiedenen Webseiten einsehen könnt oder einfach mithilfe meines Optionspreisrechners selbst berechnen könnt bzw. ein guter Broker euch die Information auch immer bereitstellt.

Ich nutze für den Optionshandel zum Beispiel den Broker Estably (bis vor kurzem noch unter „Banx Broker“ bekannt) und dort wird das Gamma als Standardinformation bei jeder Option direkt mit angezeigt. D.h. noch bevor ich überhaupt eine Option kaufe oder verkaufe, erhalte ich alle Informationen direkt von meinem Broker, die ich benötige.

Das Gamma wird bei eurem Broker dabei in der sogenannten Option Chain angezeigt. Dort findet ihr alle Call und Put Optionen geordnet nach dem jeweiligen Strike Preis für eine bestimmte Laufzeit. Neben dem Preis für jede Option werden in der Option Chain aber auch alle Greeks inklusive dem Gamma angezeigt. Hier mal ein Screenshot, wie das ganze bei Estably aussieht.

Das Bild zeigt eine beispielhafte Option Chain und welche Informationen darin bereitgestellt werden. Hervorgehoben ist der Bereich, aus dem man das Gamma von Put und Call Optionen sehen kann.

Wenn ihr auch Optionen handeln möchtet, dann kann ich euch Estably wirklich nur empfehlen. Im Hintergrund nutzt Estably Interactive Brokers was ein Tool ist, das auch von Profis genutzt wird. Entsprechend bekommt ihr dort alle Informationen, die für den Optionshandel notwendig sind und könnt euch auch alles so individuell einrichten, wie ihr möchtet.

Wenn ihr ein Depot bei Estably eröffnen wollt, dann könnt ihr das über diesen Link machen*. Das gibt euch Zugriff auf ein wirklich tolles Trading Tool, einen günstigen Broker und ihr unterstützt gleichzeitig noch meine Arbeit, weil ich bei einer Depoteröffnung eine kleine Gebühr von Estably bekomme (ohne, dass das ganze für euch teurer wird).

Aber zurück zum Thema. Auch wenn ihr das Gamma einer Option selbst nicht berechnen müsst, ist es dennoch ganz gut zu wissen, wie es berechnet wird, damit ihr besser verstehen könnt, wie sich das Gamma einer Option verändert je nachdem welche Marktveränderungen eintreten.

Mithilfe eines Optionspreismodells

Grundsätzlich gibt es verschiedene mathematische Modelle zur Preisberechnung von Optionen, allerdings hat sich in der Praxis das sogenannte „Black-Scholes-Modell“ durchgesetzt, dass nach den beiden US-Amerikaner Fischer Black und Myron Scholes benannt wurde, die dieses Modell 1973 veröffentlichten.

Das besondere am Black-Scholes Modell ist, dass es ermöglichte, die Preisberechnung einer Option auf eine mehr oder weniger einfache mathematische Formel herunterzubrechen, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.

Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt.

Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.

Das Gamma ist dabei die zweite Ableitung des Black-Scholes Modells nach dem Preis des Underlyings weswegen das Gamma auch angibt, um wie viel sich das Delta der Option ändert, wenn sich der Wert des Underlyings um 1 erhöht oder verringert.

Die Formel bzw. besser gesagt Formeln für das Black-Scholes Modell sind relativ komplex und ich möchte hier auch nicht zu sehr ins Detail gehen, weswegen ich einfach auf Wikipedia verweisen würde, wenn ihr gern mehr dazu erfahren wollt oder spielt einfach mit meinem Optionspreis-Rechner, wenn ihr ein Gefühl bekommen wollt, wie sich das Gamma einer Option unter verschiedenen Marktbedingungen verändert.

Mithilfe von Marktbeobachtungen

Das Gamma einer Option lässt sich ähnlich wie das Delta aber auch grob grob abschätzen, indem man am Markt die Preise der Option beobachtet und verfolgt, wie sich der Optionspreis bei kleinen Änderungen des Underlyings verändert.

Dazu benötigt man lediglich die Optionspreise zu drei verschiedenen Preisen des Underlyings. Zunächst betrachtet man die ersten beiden Preise des Underlyings und bildet die Differenz zwischen den entsprechenden Optionspreisen. Die Differenz teilt man dann durch die Differenz der beiden Underlying-Preise, um eine ungefähre Annäherung für das Delta für den ersten Preis des Underlyings zu erhalten. Anschließend wiederholt ihr den Vorgang für die letzten beiden Underlying-Preise, um das Delta für den zweiten Preis zu bestimmen.

Das Gamma ergibt sich nun aus der Differenz dieser beiden Delta-Werte, geteilt durch die Differenz der beiden Underlying-Preise, die für das zweite und dritte Delta verwendet wurden. Wie beim Delta sollte man diese Methode auch beim Gamma aber nur bei kleinen Preisänderungen des Underlyings anwenden, da bei zu großen Änderungen die Abweichungen vom tatsächlichen Gamma-Wert zu groß werden könnten. Empfehlenswert sind daher nur Differenzen von maximal einem Euro oder einem Dollar.

Eine andere Interpretation des Gammas

Das Gamma kann aber auch grafisch interpretiert werden, wenn man sich dazu den typischen Verlauf des Deltas einer Option in Abhängigkeit vom Kurs anschaut, wie ich es euch in der unteren Grafik anhand einer Call Option zeige.

Legt man an die Grafik eine Tangente an, also eine Linie, die die Grafik in nur einen Punkt schneidet, dann sagt der Anstieg dieser Tangente aus, wie sehr sich der Wert des Deltas verändert, wenn sich der Wert des Underlyings leicht erhöht oder verringert.

Das ist auch genau die Definition des Gammas, weswegen der Anstieg der Tangente somit auch dem Gamma der Option entspricht. Bewegt sich die Option immer mehr ins Geld hinein, dann ist der Anstieg der Tange auch immer größer bzw. nähert er sich immer mehr 1 an, genau wie wir oben auch schon beim Gamma gesehen haben.

Fällt der Wert des Underlyings aber, dann verringert sich der Anstieg der Tangente immer mehr und nähert sich null an, wie es auch bei dem Gamma der Fall ist.

Weiter oben habe ich euch schon gesagt, dass das Gamma nichts anderes ist als die zweite Ableitung der Black-Scholes Formel nach dem Preis ist und grafisch betrachtet, ist das auch die selbe Definition der Tangente.

Der Zusammenhang des Delta mit anderen Markteinflüssen

Moneyness der Option

Das Gamma einer Option ist nicht konstant und ändert sich basierend auf den aktuellen Marktgegebenheit. Den größten Einfluss auf das Gamma hat dabei der Preis des Underlyings bzw. die sogenannte „Moneyness“ der Option.

Die Grafik unten zeigt den Verlauf des Deltas (graue Linie) und des Gammas (grüne Linie) in Abhängigkeit von der Preisänderung des Underlyings bzw. der Moneyness einer Call Option.

Die Grafik zeigt dabei deutlich, dass das Gamma dann am höchsten ist, wenn sich die Option am Geld (ATM) befindet. Das führt dazu, dass am Geld bereits sehr kleine Änderungen des Kurses des Underlyings schon einen erheblichen Einfluss auf das Delta haben.

Im Gegensatz dazu ist das Gamma einer Option fast null, wenn sich die Option tief im oder außerhalb des Geldes befindet. Das bedeutet im Umkehrschluss aber auch, dass sich das Delta einer Option, die sich tief im oder außerhalb des Geldes befindet ebenfalls so gut wie nicht ändert bei kleinen Preisänderungen des Underlyings.

Restlaufzeit

Ein anderer wichtiger Einflussfaktor auf das Gamma ist die Restlaufzeit der Option. Nimmt die Restlaufzeit der Option ab, steigt das Gamma einer Option tendenziell.

Das ist für viele Optionsverkäufer auch der Grund, warum sie Optionen nie bis Laufzeitende halten, sondern schon mehrere Tage vorher zurückkaufen trotz der zusätzlichen Handelsgebühren.

Würde man seine Optionen nämlich bis Laufzeitende halten, würde das Gamma der Option wenige Tage vor Fälligkeit so groß werden, dass bereits kleine Änderungen des Preises des Underlyings einen erheblichen Einfluss auf das Gamma und damit das Delta haben und der Optionspreis sich schnell verändern kann. Wenn ihr gern mehr darüber erfahren wollt, wann man Optionen wieder zurückkaufen sollte, dann lest euch doch am besten diesen Artikel von mir durch.

Volatilität

Das Gamma ist aber auch sehr stark von der Volatilität einer Option abhängig. Befindet sich eine Option am Geld, dann ist das Gamma dieser Option höher, je niedriger die implizite Volatilität des Underlyings ist. Befindet sich eine Option aber im oder außerhalb des Geldes, dann ist die Beziehung zwischen Gamma und Volatilität genau umgekehrt.

Bei Optionen, die sich im oder außerhalb des Geldes befinden, ist das Gamma umso höher, je höher die implizite Volatilität des Underlyings ist. Den Zusammenhang könnt ihr sehr gut in der folgenden Grafik sehen.

Die Abhängigkeit des Gammas von der Volatilität macht intuitiv aber auch Sinn, wenn man sich das Zusammenspiel von Volatilität und Delta noch einmal vor Augen führt.

Stellt euch dafür einfach eine Option mit geringer Volatilität des Underlyings vor. Aufgrund der geringen Vola, hat die Optionen auch nur einen geringen Zeitwert und aufgrund des geringen Zeitwerts steigt das das Delta der Option schnell an, je mehr sich die Option ins Geld bewegt. Genau dieser schnelle Anstieg des Deltas bedeutet ja, dass das Gamma entsprechend auch sehr hoch sein muss.

Der Anstieg des Deltas ist somit also höher als bei Optionen, deren Underlyings eine hohe implizite Volatilität haben.

Als allgemeine Faustregel gilt, dass das Gamma einer Option umso konstanter ist, je höher die Volatilität des Underlyings ist. Bei niedriger Volatilität des Underlyings ist das Gamma am Geld am höchsten und fällt ab, je tiefer sich die Option ins Geld oder aus dem Geld heraus bewegt.

Diese Faustregel ist besonders interessant, wenn man eine Delta-neutrale Position haben möchte. Mehr dazu erkläre ich euch in meinem Artikel zum Thema „Delta Hedging“.

Der Schlüssel zum Erfolg im Optionshandel ist die Greeks einer Option zu verstehen und der vielleicht wichtigste Greek von allen ist das Delta. Was sich hinter dem Delta einer Option verbirgt und wie ihr es in euren täglichen Optionshandel nutzen könnt, verrate ich euch in diesen Artikel.

Dieser Artikel behandelt das Delta einer Option im Detail. Wenn ihr gern einen allgemeineren Überblick über alle Griechen einer Optionen haben wollt, dann könnt ihr euch auch diesen Artikel von mir durchlesen.

Was ist das Delta einer Option?

Das Delta einer Option ist für viele Optionshändler der wahrscheinlich wichtigste Greek. Es gibt an, um wie viel sich der Preis der Option ändert, wenn der Kurs des Underlyings um eine Währungseinheit steigt oder fällt und gibt Optionshändlern damit Auskunft darüber, wie sehr die Wertentwicklung einer Option von den Preisbewegungen des Underlying abhängig ist.

Der Wert des Deltas kann immer nur zwischen -1 und +1 liegen wobei für Calls und Puts immer gilt:

• Bei Calls ist das Delta der Option immer zwischen 0 bis 1
• Bei Puts ist das Delta der Option immer zwischen -1 bis 0

Hat eine Call Option somit ein Delta von 0,5, dann steigt der Wert der Option um 50 Cent, wenn das Underlying um einen Euro im Wert steigt. Hat eine Put Option im Gegensatz dazu ein Delta von -0,5, dann fällt der Wert des Puts um 50 Cent, wenn der Preis des Underlyings um einen Euro steigt.

Die Dezimalschreibweiße ist zwar die mathematisch korrekte Art, das Delta zu beschreiben aber in der Praxis sagt bzw. schreibt man selten, dass eine Option ein Delta von 0,5 oder -0,5 hat, sondern man sagt stattdessen, dass eine Option ein Delta von 50 oder -50 hat.

Ein Delta von 10 bedeutet somit, dass eine Call Option 10 Cent im Wert steigt, wenn das Underlying einen Euro im Wert ansteigt.

Ganz wichtig ist allerdings, dass solche Rechnungen nur Annäherungen an die tatsächliche Preisänderung des Optionspreises sind. Das Delta einer Option ist schließlich keine statische Kennzahl und kann durch viele Faktoren beeinflusst werden (mehr dazu gleich) und entsprechend kann man die Preisänderung einer Option mithilfe des Deltas nur für geringe Preisänderungen des Underlyings berechnen. Lasst mich das ganze einfach anhand eines kleines Beispiels verdeutlichen.

Wie sehr sich das Delta einer Option durch eine Änderung des Underlying-Preises verändert, gibt das sogenannte Gamma an. Das ist ein weitere Greek, den ich euch in einem anderen Artikel erklären werde aber ihr könnt ihn euch einfach als das Delta des Deltas vorstellen. D.h. das Delta gibt an, wie sehr sich der Preis der Option verändert, wenn sich der Preis des Underlyings ändert und das Gamma gibt an, wie sehr sich das Delta ändert, wenn sich der Preis des Underlyings ändert.

Von allen Faktoren, die das Delta beeinflussen (mehr dazu gleich) hat der Preis des Underlyings bzw. die sogenannte „Moneyness“ den größten Einfluss auf das Delta.

Als allgemeine Faustregel gilt, dass Optionen, die sich im Geld (ITM) befinden, ein Delta größer 50 haben und Optionen, die sich außerhalb des Geldes (OTM) befinden ein Delta kleiner 50 haben. Optionen, die sich am Geld (ATM) befinden, haben ein Delta von circa 50.

Umso mehr sich eine Call Option im Geld befindet, desto mehr nähert sich das Delta der Option an 1 an und je mehr sich eine Call Option außerhalb des Geldes befindet, desto stärker nähert sich das Delta der Option an 0 an. Bei Put Optionen verhält es sich genauso, allerdings nähert sich das Delta von Put Optionen immer mehr -1 an, je stärker die Option sich ins Geld bewegt und immer näher 0, je weiter sich die Option aus dem Geld bewegt.

Beträgt der Marktpreis des Underlyings genau dem Strikepreis einer Option (also die Option ist exakt am Geld), dann ist das Delta der Option allerdings in aller Regel nicht genau 50. Überlicherweise haben Call Optionen in dem Fall ein Delta von leicht mehr als 50 und Put Optionen ein Delta von leicht weniger als 50.

Der Effekt bzw. Abstand zwischen dem Delta einer Call und Put Option mit gleichem Ausübunsgpreis wird dabei umso größer je länger die Laufzeit der Option ist (mehr dazu weiter unten) und je höher der aktuelle Marktzins ist. Grund dafür ist die sogenannte „Put-Call-Parität“ die ich euch in einem anderen Artikel erklären werde.

Habt ihr übrigens eine Position, die aus mehreren Optionen besteht, dann ist das Delta dieser Position die Summe aller Deltas der Optionen, die ihr haltet. Handelt ihr also komplexere Optionsstrategien, dann kann es schnell auch kompliziert werden zu wissen, wie sich das Delta bei Kursschwankungen bewegen wird. Damit ihr nicht den Überblick verliert, habe ich deshalb für euch ein Cheat Sheet erstellt, das euch direkt zeigt, wie sich das Delta für verschiedene Optionsstrategien verändert, je nachdem wie sich der Markt bewegt. Ihr könnt es euch hier gratis herunterladen.

Die Berechnung des Deltas einer Option

Um das Delta einer Option zu berechnen, gibt es grundsätzlich zwei Möglichkeiten. Die korrekte Variante ist, dass man das Delta mithilfe eines Optionspreismodells berechnet und die weniger komplizierte Variante ist die Berechnung mithilfe von Marktdaten. Ich erkläre euch gleich beide Varianten etwas genauer, allerdings will ich an dieser Stelle auch hinweisen, dass es in aller Regel gar nicht notwendig ist, dass ihr das Delta einer Option selbst berechnet, weil ihr diese Information auch online auf verschiedenen Webseiten einsehen könnt oder einfach mithilfe meines Optionspreisrechners selbst berechnen könnt bzw. ein guter Broker euch die Information auch immer bereitstellt.

Ich nutze für den Optionshandel zum Beispiel den Broker Estably (bis vor kurzem noch unter „Banx Broker“ bekannt) und dort wird das Delta als Standardinformation bei jeder Option direkt mit angezeigt. D.h. noch bevor ich überhaupt eine Option kaufe oder verkaufe, erhalte ich alle Informationen direkt von meinem Broker, die ich benötige.

Das Delta wird bei eurem Broker dabei in der sogenannten Option Chain angezeigt. Dort findet ihr alle Call und Put Optionen geordnet nach dem jeweiligen Strike Preis für eine bestimmte Laufzeit. Neben dem Preis für jede Option werden in der Option Chain aber auch alle Greeks inklusive dem Delta angezeigt. Hier mal ein Screenshot, wie das ganze bei Estably aussieht.

Wenn ihr auch Optionen handeln möchtet, dann kann ich euch Estably wirklich nur empfehlen. Im Hintergrund nutzt Estably Interactive Brokers was ein Tool ist, das auch von Profis genutzt wird. Entsprechend bekommt ihr dort alle Informationen, die für den Optionshandel notwendig sind und könnt euch auch alles so individuell einrichten, wie ihr möchtet.

Wenn ihr ein Depot bei Estably eröffnen wollt, dann könnt ihr das über diesen Link machen*. Das gibt euch Zugriff auf ein wirklich tolles Trading Tool, einen günstigen Broker und ihr unterstützt gleichzeitig noch meine Arbeit, weil ich bei einer Depoteröffnung eine kleine Gebühr von Estably bekomme (ohne, dass das ganze für euch teurer wird).

Aber zurück zum Thema. Auch wenn ihr das Delta einer Option selbst nicht berechnen müsst, ist es dennoch ganz gut zu wissen, wie es berechnet wird, damit ihr besser verstehen könnt wie sich das Delta einer Option verändert je nachdem welche Marktveränderungen eintreten.

Mithilfe eines Optionspreismodells

Grundsätzlich gibt es verschiedene mathematische Modelle zur Preisberechnung von Optionen, allerdings hat sich in der Praxis das sogenannte „Black-Scholes-Modell“ durchgesetzt, dass nach den beiden US-Amerikaner Fischer Black und Myron Scholes benannt wurde, die dieses Modell 1973 veröffentlichten.

Das besondere am Black-Scholes Modell ist, dass es ermöglichte, die Preisberechnung einer Option auf eine mehr oder weniger einfache mathematische Formel herunterzubrechen, die es jedem Händler mit einem Taschenrechner ermöglichte schnell und zügig eine Option zu preisen.

Die mathematische Formel besitzt nun verschiedene Variablen und diese Variablen bzw. deren Ableitungen (entschuldigt bitte, wenn es jetzt zu mathematisch wird, aber eine Ableitung ist nichts anderes als die Frage „Um wieviel ändert sich Wert X, wenn sich Wert Y um 1 erhöht oder verringert“) wurden durch Black und Scholes in ihrer Formel durch griechische Buchstaben dargestellt.

Genau diese Variablen und Ableitungen sind nun das, was die Griechen bzw. Greeks repräsentieren und das ist der Grund warum man diese Kennzahlen als „Die Griechen“ bezeichnet.

Das Delta ist dabei die erste Ableitung des Black-Scholes Modells nach dem Preis des Underlyings weswegen das Delta auch angibt, um wie viel sich der Preis der Option ändert, wenn sich der Wert des Underlyings um 1 erhöht oder verringert.

Die Formel bzw. besser gesagt Formeln für das Black-Scholes Modell sind relativ komplex und ich möchte hier auch nicht zu sehr ins Detail gehen, weswegen ich einfach auf Wikipedia verweisen würde, wenn ihr gern mehr dazu erfahren wollt.

Mithilfe von Marktbeobachtungen

Man kann das Delta aber auch grob schätzen, indem man einfach am Markt die Preise einer Option beobachtet und schaut, wie der Preis der Option auf kleine Änderungen des Underlyings reagiert.

Ihr benötigt dazu einfach nur zwei unterschiedliche Preise des Underlyings und schaut dann wie bei beiden Preisen der Preis der Option war. Bildet mit diesem Wissen dann einfach die Differenz zwischen den beiden Optionspreisen und den beiden Preisen des Underlyings und teilt dann die Differenz des Optionspreises durch die Differenz des Underlying-Preises.

Das Ergebnis ist das Delta, allerdings solltet ihr diese Methode nur bei kleinen Preisänderungen des Underlyings verwenden, weil ihr bei zu großen Änderungen ansonsten zu große Abweichungen zum tatsächlichen Delta bekommt. Nutzt also nur Differenzen von maximal einem Euro oder einem Dollar.

Andere Interpretationen des Delta

Wie oben schon erwähnt, beschreibt das Delta einer Option wie stark sich der Wert einer Option verändert, wenn sich der Preis des Underlyings um eine Währungseinheit verändert. Es gibt allerdings auch noch weitere Möglichkeiten, wie das Delta einer Option interpretiert werden kann.

1. Das Äquivalent zu einem Direktinvestment in das Underlying

Das Delta gibt an, wie stark sich eine Option in Abhängigkeit vom Underlying ändert. Beträgt das Delta 0, dann ändert sich der Optionspreis überhaupt nicht bei einer Änderung des Underlying-Preises und bei einem Delta von 1, dann verändert sich der Wert der Option um einen Euro, wenn sich der Wert des Underlying um einen Euro bewegt.

Nach dieser Logik kann man also sagen, dass das Underlying selbst immer ein Delta von 1 hat. Immer wenn sich der Kurs des Underlyings um einen Euro bewegt, dann ist das Underlying auch einen Euro mehr oder weniger wert.

Besitze ich eine Call Option mit einem Delta von 60, dann steigt der Wert meiner Option um 60 Cent, wenn sich das Underlying um einen Euro erhöht. Da Optionen in aller Regel aber 100 Aktien umfassen, würde der Wert der Call Option also in dem Fall um 60 EUR steigen, wenn der Kurs des Underlyings um einen Euro steigt.

Die Wertentwicklung meiner Option ist in diesem Fall also genau so als würde ich genau 60 Aktien des Underylings besitzen. Steigt der Wert der 60 Aktie um einen Euro, dann mache ich mit den Aktien 60 Euro Gewinn und steigt der Wert der Aktie um einen Euro, dann steigt auch der Wert der Option um 60 EUR.

Das Delta einer Option entspricht somit auch dem Äquivalent zu einem Direktinvestment in das Underlying. Diese Interpretation ist vor allem beim sogenannten „Delta Hedging“ wichtig, dass ich euch in diesem Artikel genauer erkläre.

2. Die Wahrscheinlichkeit, dass sich die Option am Ende der Laufzeit im Geld befindet

In der Praxis wird das Delta einer Option auch als grobe Annäherung dafür genutzt, wie wahrscheinlich es ist, dass sich die Option am Ende der Laufzeit im Geld befindet oder nicht. Eine Call Option mit einem Delta von 75 hätte in diesem Fall also grob eine Wahrscheinlichkeit von 75%, dass sie sich bei Laufzeitende im Geld befindet.

Das macht intuitiv erst einmal auch Sinn. Optionen mit einem hohen Delta (größer 50) befinden sich schließlich schon im Geld und haben deswegen auch eine höhere Wahrscheinlichkeit am Ende der Laufzeit weiterhin im Geld zu sein. Optionen mit niedrigem Delta (kleiner 50) befinden sich aktuell außerhalb des Geldes und haben dementsprechend auch nur eine geringere Wahrscheinlichkeit sich ins Geld zu bewegen.

Mathematisch betrachtet, ist diese Faustregel aber wirklich nicht mehr als eine ganz grobe Annäherung und ihr solltet sie mir Vorsicht genießen. Weil ich die Praktiker unter euch nicht mit Mathematik langweilen möchte, müsst ihr den folgenden Text aufklappen, um zu verstehen warum das so ist, allerdings kann ich jedem Optionshändler nur empfehlen, diesen Zusammenhang unbedingt zu verstehen.

Warum das Delta nur eine Annäherung an die ITM Wahrscheinlichkeit ist

In der Black-Scholes-Formel entspricht das Delta der Option dem Wert der Normalverteilung für den Faktor D1. Die Wahrscheinlichkeit, dass eine Option im Geld landet ist wiederum der Wert der Normalverteilung für den Faktor D1 abzüglich der impliziten Volatilität multipliziert mit der Wurzel aus der Restlaufzeit.

D.h. rein mathematisch betrachtet ist die Wahrscheinlichkeit für eine Option im Geld zu landen und deren Delta zwar etwas komplett anderes aber auch nicht so unterschiedlich. Die beiden Werte unterscheiden sich dabei umso mehr, je länger die Laufzeit der Option ist und je größer die implizite Volatilität ist.

Für kurze Laufzeiten und Optionen mit geringer impliziter Volatilität ist das Delta also eine sehr gute Annäherung für die Wahrscheinlichkeit einer Option im Geld zu landen aber je länger die Laufzeit ist und je höher die Volatilität ist, desto mehr solltet ihr das ganze mit Vorsicht genießen.

Wie gut diese Faustregel in der Praxis zutrifft, habe ich einmal selbst mithilfe von über 500.000 Optionen analysiert. Die folgende Grafik zeigt euch dabei auf der Y-Achse, wie hoch das Delta zum Kaufzeitpunkt der Option war (und entsprechend die grobe Wahrscheinlichkeit, dass die Option im Geld landet) und auf der X-Achse wie viele Optionen mit dem Delta am Ende wirklich im Geld landete.

Die rote Linie zeigt euch dabei den Verlauf, wenn das Delta einer Option die Wahrscheinlichkeit im Geld zu landen immer korrekt angeben würde. Die grüne Linie zeigt euch aber stattdessen die tatsächliche Wahrscheinlichkeit aller Call Optionen, die ich untersucht habe und die blaue Linie zeigt euch die tatsächliche Wahrscheinlichkeit aller Put Optionen.

Ihr seht dabei schön deutlich, dass vor allem bei Optionen, die sich entweder weit im oder weit außerhalb des Geldes befinden, dass Delta eine sehr gute Annäherung für die Wahrscheinlichkeit ist, dass die Option im Geld landet.

Das Delta gibt die Wahrscheinlichkeit aber umso schlechter an, je näher sich eine Option am Geld befindet und zur großen Überraschung gibt es dabei einen sehr wichtigen Unterschied zwischen Put und Call Optionen.

Bei ATM Call Optionen unterschätzt das Delta nämlich tendenziell die Wahrscheinlichkeit, dass eine Option im Geld landet. D.h. ATM Call Optionen landen viel häufiger im Geld, als es das Delta vermuten lässt und bei Put Optionen ist es genau anders herum. Für Put ATM Optionen überschätzt das Delta nämlich tendenziell die Wahrscheinlich, dass eine Option im Geld landet. D.h. Put Optionen landen viel seltener im Geld, als es das Delta vermuten lässt.

3. Der Anstieg der Tangente des Gewinn-und-Verlust Profils der Option

Das Delta kann aber auch grafisch interpretiert werden, wenn man sich dazu den typischen Verlauf des Gewinn und Verlustes einer Option anschaut, wie ich es euch in der unteren Grafik anhand einer Call Option zeige.

Legt man an die Grafik eine Tangente an, also eine Linie, die die Grafik in nur einen Punkt schneidet, dann sagt der Anstieg dieser Tangente aus, wie sehr sich der Wert der Option verändert, wenn sich der Wert des Underlyings leicht erhöht oder verringert.

Das ist auch genau die Definition des Deltas, weswegen der Anstieg der Tangente somit auch dem Delta der Option entspricht. Bewegt sich die Option immer mehr ins Geld hinein, dann ist der Anstieg der Tange auch immer größer bzw. nähert er sich immer mehr 1 an, genau wie wir oben auch schon beim Delta gesehen haben.

Fällt der Wert des Underlyings aber, dann verringert sich der Anstieg der Tangente immer mehr und nähert sich null an, wie es auch bei dem Delta der Fall ist.

Weiter oben habe ich euch schon gesagt, dass das Delta nichts anderes ist als die erste Ableitung der Black-Scholes Formel nach dem Preis ist und grafisch betrachtet, ist das auch die selbe Definition der Tangente.

Der Zusammenhang des Delta mit anderen Markteinflüssen

Volatilität

Die Volatilität, also die übliche Schwankungsbreite des Underlyings, hat einen großen Einfluss auf das Delta einer Option. Ist die Volatilität gering, dann ist das Delta von In-the-Money Optionen, höher und für Out-of-the-Money Optionen niedriger als bei einer Option mit hoher Volatilität des Underlyings. Ihr könnt den Zusammenhang sehr gut in der folgenden Grafik sehen.

Die Grafik zeigt euch dabei den Verlauf des Delta zweier Call Optionen in Abhängigkeit von der Moneyness der Option und deren Volatilität.

Die rote Linie ist dabei die Option mit hoher Volatilität und die blaue Linie die Option mit der niedrigen Volatilität. Beide Optionen beziehen sich auf das selbe Underlying, haben die selbe Laufzeit und in beiden Fällen ist der Preis des Underlyings gerade 50 EUR. Das einzige, was variabel ist, ist der Strike Preis.

Ihr seht dabei deutlich, dass die Option mit der geringen Volatilität ein höheres Delta im Vergleich zu der Option mit hoher Volatilität hat, wenn die Option im Geld ist aber dafür ein geringeres Delta, wenn die Option nicht im Geld ist.

Restlaufzeit

Die Restlaufzeit einer Option hat ebenso einen großen Einfluss auf das Delta. Ist die Restlaufzeit nur noch kurz , dann ist das Delta von In-the-Money Optionen höher und für Out-of-the-Money Optionen niedriger als bei einer Option mit einer längeren Restlaufzeit. Ihr könnt den Zusammenhang wieder sehr gut in der folgenden Grafik sehen.

Die Grafik zeigt euch dabei wieder den Verlauf des Deltas von drei Call Optionen in Abhängigkeit von der Moneyness der Option und deren Restlaufzeit.

Die blaue Linie ist dabei die Option mit der kürzesten Restlaufzeit (3 Monate), die grüne Linie hat eine etwas längere Laufzeit (6 Monate) und die rote Linie hat die längste Laufzeit (12 Monate).

Ihr könnt dabei erkennen, dass das Delta einer Option im Geld umso höher ist, je kürzer die Restlaufzeit ist und für OTM Option dafür umso niedriger ist, je kürzer die Restlaufzeit ist.

Allgemein kann man sagen, dass umso länger die Laufzeit einer Option ist, desto stärker nähert sich das Delta für alle Optionen (im Geld, am Geld und aus dem Geld) an 0,5 an.

Besonders deutlich kann man diesen Zusammenhang auch in der nächsten Grafik sehen.

Die Grafik zeigt euch diesmal das Delta einer Call Option an, die dich gerade am Geld befindet. In der Grafik werden alle Einflussgrößen gleich gelassen und nur die Restlaufzeit verändert und ihr könnt sehen, was das für einen Einfluss auf das Delta der Call Option hat.

Während das Delta der ATM Call Option bei langer Laufzeit noch über 50 liegt, nähert es sich bei kürzer werdender Laufzeit immer mehr einem Delta von genau 50 an. Ihr seht aber auch, dass sich das Delta einer Option umso schneller verringert, je näher man sich an das Laufzeitende bewegt.

Ihr müsst euch also merken, dass selbst wenn alle Faktoren einer Option gleich bleiben und sich auch der Kurs des Underlyings nicht verändert, das Delta sich dennoch verändert, einfach nur weil sich mit jeden Tag die Restlaufzeit der Option verkürzt.